Descubre la teoría de conjuntos y sus fórmulas clave
La teoría de conjuntos es una rama de las matemáticas que se dedica al estudio de los conjuntos, sus propiedades y sus relaciones. Fue desarrollada en el siglo XIX por el matemático alemán Georg Cantor, y desde entonces se ha convertido en una herramienta indispensable en muchos campos de la ciencia, la tecnología y la ingeniería.
En este artículo, vamos a explorar algunos conceptos clave de la teoría de conjuntos y sus fórmulas más importantes. Si eres un estudiante de matemáticas o simplemente tienes curiosidad por aprender más sobre este fascinante tema, ¡sigue leyendo!
¿Qué es un conjunto?
Antes de entrar en las fórmulas de la teoría de conjuntos, es importante entender lo que es un conjunto. Un conjunto es una colección de objetos, llamados elementos, que comparten una o más características en común. Por ejemplo, el conjunto de los números pares es una colección de números que se pueden dividir en dos partes iguales, mientras que el conjunto de las frutas es una colección de alimentos que crecen en árboles o arbustos.
Operaciones básicas de conjuntos
La teoría de conjuntos se basa en varias operaciones básicas, que se utilizan para manipular conjuntos y crear conjuntos nuevos. Estas operaciones son la unión, la intersección, la diferencia y el complemento.
La unión de dos conjuntos A y B es el conjunto que contiene todos los elementos que pertenecen a A, a B o a ambos conjuntos. Se denota por A ∪ B.
La intersección de dos conjuntos A y B es el conjunto que contiene todos los elementos que pertenecen tanto a A como a B. Se denota por A ∩ B.
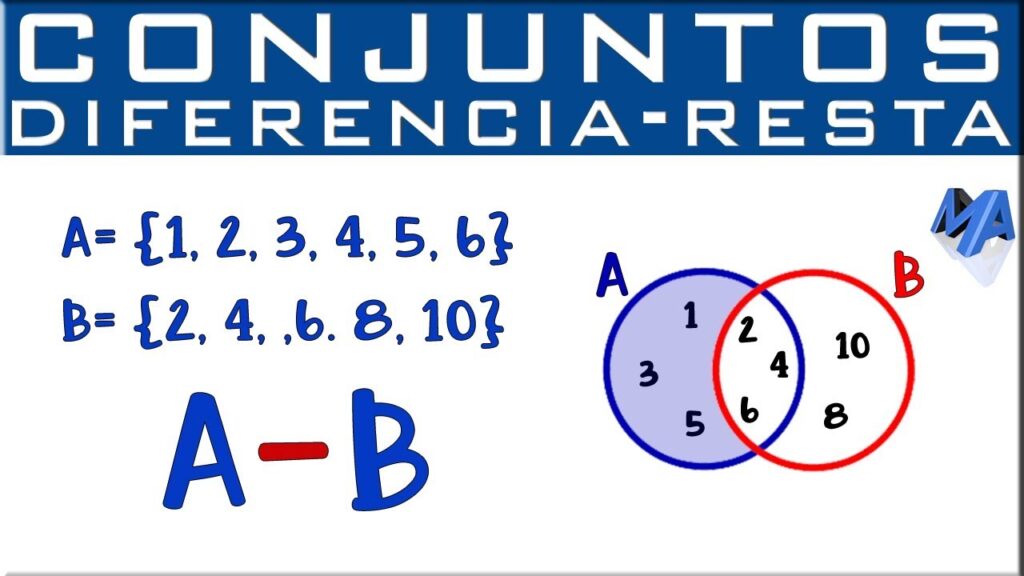
La diferencia de dos conjuntos A y B es el conjunto que contiene todos los elementos que pertenecen a A pero no a B. Se denota por A - B.
El complemento de un conjunto A es el conjunto que contiene todos los elementos que no pertenecen a A. Se denota por A'.
Fórmulas clave de la teoría de conjuntos
Ahora que hemos repasado las operaciones básicas de conjuntos, podemos pasar a las fórmulas clave de la teoría de conjuntos. Estas fórmulas se utilizan para simplificar o demostrar relaciones entre conjuntos.
Identidad de la unión
La identidad de la unión establece que la unión de un conjunto con el conjunto vacío es igual al conjunto original. Es decir:
A ∪ ∅ = A
Esto se debe a que la unión de un conjunto con el conjunto vacío no añade ningún elemento nuevo al conjunto original.
Identidad de la intersección
La identidad de la intersección establece que la intersección de un conjunto con el conjunto universo es igual al conjunto original. Es decir:
A ∩ U = A
Esto se debe a que cualquier elemento que pertenece al conjunto A también pertenece al conjunto universo.
Conmutatividad de la unión e intersección
La conmutatividad de la unión e intersección establece que el orden en que se unen o se intersectan dos conjuntos no afecta al resultado final. Es decir:
A ∪ B = B ∪ A
A ∩ B = B ∩ A
Asociatividad de la unión e intersección
La asociatividad de la unión e intersección establece que el resultado de unir o intersectar tres o más conjuntos no depende del orden en que se realizan las operaciones. Es decir:
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
Distributividad de la unión sobre la intersección
La distributividad de la unión sobre la intersección establece que la unión de un conjunto con la intersección de dos conjuntos es igual a la intersección de la unión del conjunto con cada uno de los conjuntos. Es decir:
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Distributividad de la intersección sobre la unión
La distributividad de la intersección sobre la unión establece que la intersección de un conjunto con la unión de dos conjuntos es igual a la unión de la intersección del conjunto con cada uno de los conjuntos. Es decir:
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Leyes de De Morgan
Las leyes de De Morgan establecen que el complemento de la unión de dos conjuntos es igual a la intersección de los complementos de los conjuntos, y que el complemento de la intersección de dos conjuntos es igual a la unión de los complementos de los conjuntos. Es decir:
(A ∪ B)' = A' ∩ B'
(A ∩ B)' = A' ∪ B'
Conclusión
La teoría de conjuntos es una herramienta esencial en muchos campos de la matemática y la ciencia, y las fórmulas clave que hemos repasado aquí son fundamentales para entenderla. Al dominar estas fórmulas y operaciones, los estudiantes pueden resolver problemas complejos y demostrar relaciones entre los conjuntos con facilidad.
Preguntas frecuentes
¿Qué es un conjunto?
Un conjunto es una colección de objetos, llamados elementos, que comparten una o más características en común.
¿Cuáles son las operaciones básicas de conjuntos?
Las operaciones básicas de conjuntos son la unión, la intersección, la diferencia y el complemento.
¿Para qué se utiliza la teoría de conjuntos?
La teoría de conjuntos se utiliza para manipular conjuntos y crear conjuntos nuevos, y es esencial en muchos campos de la ciencia, la tecnología y la ingeniería.
¿Qué son las leyes de De Morgan?
Las leyes de De Morgan establecen que el complemento de la unión de dos conjuntos es igual a la intersección de los complementos de los conjuntos, y que el complemento de la intersección de dos conjuntos es igual a la unión de los complementos de los conjuntos.
¿Por qué es importante aprender la teoría de conjuntos?
La teoría de conjuntos es una herramienta esencial en muchos campos de la matemática y la ciencia, y las fórmulas clave que hemos repasado aquí son fundamentales para entenderla. Al dominar estas fórmulas y operaciones, los estudiantes pueden resolver problemas complejos y demostrar relaciones entre los conjuntos con facilidad.
Deja una respuesta