Descubre la teoría de conjuntos de manera fácil: ¡Aprende desde cero!

La teoría de conjuntos es una herramienta fundamental en las matemáticas, y su comprensión puede ser un poco compleja para algunas personas. Sin embargo, no tiene por qué ser así. En este artículo, te enseñaremos a entender la teoría de conjuntos desde cero, de manera fácil y sencilla. ¡Vamos a empezar!

¿Qué es la teoría de conjuntos?

La teoría de conjuntos es una rama de las matemáticas que se dedica al estudio de los conjuntos, que son colecciones de objetos o elementos. Por ejemplo, un conjunto puede estar formado por los números 1, 2 y 3, o por las letras A, B y C. En la teoría de conjuntos, se estudian las propiedades de los conjuntos y las relaciones que pueden establecerse entre ellos.

Elementos de un conjunto

Un conjunto está formado por elementos, que pueden ser números, letras, objetos, animales, personas, o cualquier cosa que se quiera agrupar. Los elementos de un conjunto se representan entre llaves, y se separan por comas. Por ejemplo, el conjunto de los números pares menores que 10 se escribe así:

{2, 4, 6, 8}

Relaciones entre conjuntos

En la teoría de conjuntos, se pueden establecer diferentes relaciones entre los conjuntos. Algunas de las más comunes son:

- Unión: La unión de dos conjuntos es el conjunto que contiene todos los elementos que pertenecen a uno u otro conjunto. Por ejemplo, si A = {1, 2, 3} y B = {2, 4, 6}, entonces la unión de A y B es el conjunto {1, 2, 3, 4, 6}.

- Intersección: La intersección de dos conjuntos es el conjunto que contiene los elementos que pertenecen a ambos conjuntos. Por ejemplo, si A = {1, 2, 3} y B = {2, 4, 6}, entonces la intersección de A y B es el conjunto {2}.

- Complemento: El complemento de un conjunto es el conjunto de todos los elementos que no pertenecen al conjunto original. Por ejemplo, si A = {1, 2, 3} y U es el conjunto universo (que contiene todos los elementos posibles), entonces el complemento de A es el conjunto U-A = {4, 5, 6, ...}.

Diagramas de Venn

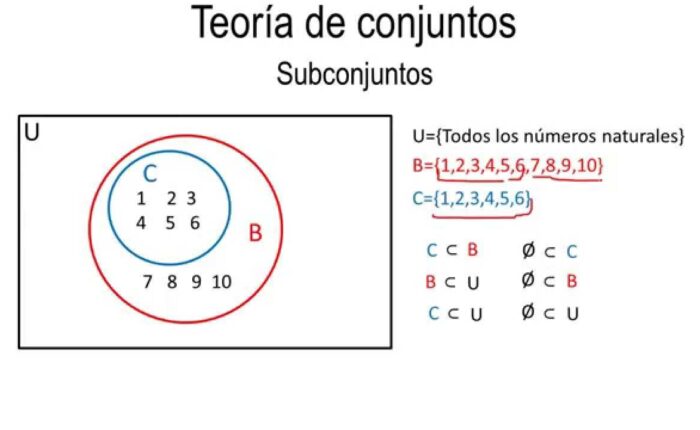
Los diagramas de Venn son una herramienta útil para representar las relaciones entre conjuntos. En un diagrama de Venn, cada conjunto se representa como un círculo, y las intersecciones se muestran como regiones superpuestas. Por ejemplo, el diagrama de Venn de los conjuntos A y B que hemos visto antes sería así:


Operaciones con conjuntos

En la teoría de conjuntos, se pueden realizar diferentes operaciones para combinar o modificar conjuntos. Algunas de las más comunes son:

- Inclusión: Un conjunto A está incluido en otro conjunto B (se escribe A ⊆ B) si todos los elementos de A también pertenecen a B.

- Diferencia: La diferencia de dos conjuntos A y B es el conjunto que contiene todos los elementos de A que no pertenecen a B. Se escribe A-B.

- Producto cartesiano: El producto cartesiano de dos conjuntos A y B es el conjunto de todos los pares ordenados (a, b) donde a pertenece a A y b pertenece a B. Se escribe A x B.

Conjuntos numéricos

En la teoría de conjuntos, existen diferentes conjuntos numéricos que se utilizan con frecuencia. Algunos de los más comunes son:

- Conjunto de los números naturales (N): Este conjunto incluye todos los números enteros positivos, es decir, 1, 2, 3, 4, ...

- Conjunto de los números enteros (Z): Este conjunto incluye todos los números enteros, positivos, negativos y cero, es decir, ..., -2, -1, 0, 1, 2, ...

- Conjunto de los números racionales (Q): Este conjunto incluye todos los números que pueden expresarse como una fracción, es decir, números que pueden representarse como p/q, donde p y q son enteros y q no es cero.

- Conjunto de los números reales (R): Este conjunto incluye todos los números racionales e irracionales, es decir, todos los números que pueden representarse en la recta numérica.

Conclusión

La teoría de conjuntos puede parecer un poco complicada al principio, pero con un poco de práctica y paciencia, puede resultar muy útil en muchas ramas de las matemáticas y otras áreas de conocimiento. Esperamos que este artículo te haya ayudado a entender los conceptos básicos de la teoría de conjuntos, y que te haya animado a seguir explorando y aprendiendo más sobre este fascinante tema.

Preguntas frecuentes

1. ¿Qué es un conjunto?

Un conjunto es una colección de objetos o elementos.

2. ¿Para qué sirve la teoría de conjuntos?

La teoría de conjuntos se utiliza en muchas ramas de las matemáticas y otras áreas de conocimiento para estudiar las propiedades de los conjuntos y las relaciones que pueden establecerse entre ellos.

3. ¿Qué es la unión de dos conjuntos?

La unión de dos conjuntos es el conjunto que contiene todos los elementos que pertenecen a uno u otro conjunto.

4. ¿Qué es el complemento de un conjunto?

El complemento de un conjunto es el conjunto de todos los elementos que no pertenecen al conjunto original.

5. ¿Qué es el producto cartesiano de dos conjuntos?

El producto cartesiano de dos conjuntos es el conjunto de todos los pares ordenados (a, b) donde a pertenece a uno de los conjuntos y b pertenece al otro.