Descubre la representación visual de la teoría de conjuntos
¿Te has preguntado alguna vez cómo se puede representar visualmente la teoría de conjuntos? Si es así, este artículo es para ti. La teoría de conjuntos es una rama fundamental de las matemáticas que se encarga del estudio de los conjuntos, sus propiedades y las relaciones entre ellos. La representación visual de la teoría de conjuntos es una herramienta poderosa que nos permite entender mejor los conceptos fundamentales de esta teoría. En este artículo, te explicaremos cómo funciona la representación visual de la teoría de conjuntos y cómo puedes aplicarla en tus propios estudios de matemáticas.
- ¿Qué es la teoría de conjuntos?
- ¿Qué es la representación visual de la teoría de conjuntos?
- ¿Cómo funciona la representación visual de la teoría de conjuntos?
- ¿Cómo se aplican los diagramas de Venn en la teoría de conjuntos?
- ¿Cómo se pueden utilizar los diagramas de Venn en otras áreas de las matemáticas?
- Conclusión
- Preguntas frecuentes
¿Qué es la teoría de conjuntos?
Antes de entrar en detalles sobre la representación visual de la teoría de conjuntos, es importante tener una comprensión básica de lo que es la teoría de conjuntos. La teoría de conjuntos es una rama de las matemáticas que se ocupa del estudio de los conjuntos, que son colecciones de objetos. Estos objetos pueden ser números, letras, palabras o cualquier otra cosa que se pueda agrupar en una colección. La teoría de conjuntos estudia las propiedades de los conjuntos y las relaciones entre ellos.
¿Qué es la representación visual de la teoría de conjuntos?
La representación visual de la teoría de conjuntos es una herramienta que permite representar los conjuntos y sus relaciones de una manera visual. Esta representación se realiza mediante diagramas de Venn, que son diagramas que muestran los conjuntos como círculos o elipses superpuestos. Cada conjunto se representa por un círculo o elipse, y las relaciones entre los conjuntos se representan mediante la superposición de los círculos o elipses.
¿Cómo funciona la representación visual de la teoría de conjuntos?
Para entender cómo funciona la representación visual de la teoría de conjuntos, es útil conocer algunos conceptos básicos. En primer lugar, es importante entender lo que es la inclusión de conjuntos. Si un conjunto A está incluido en un conjunto B, significa que todos los elementos de A también están en B. Esto se representa mediante un círculo o elipse dentro de otro círculo o elipse, como se muestra en la siguiente figura:

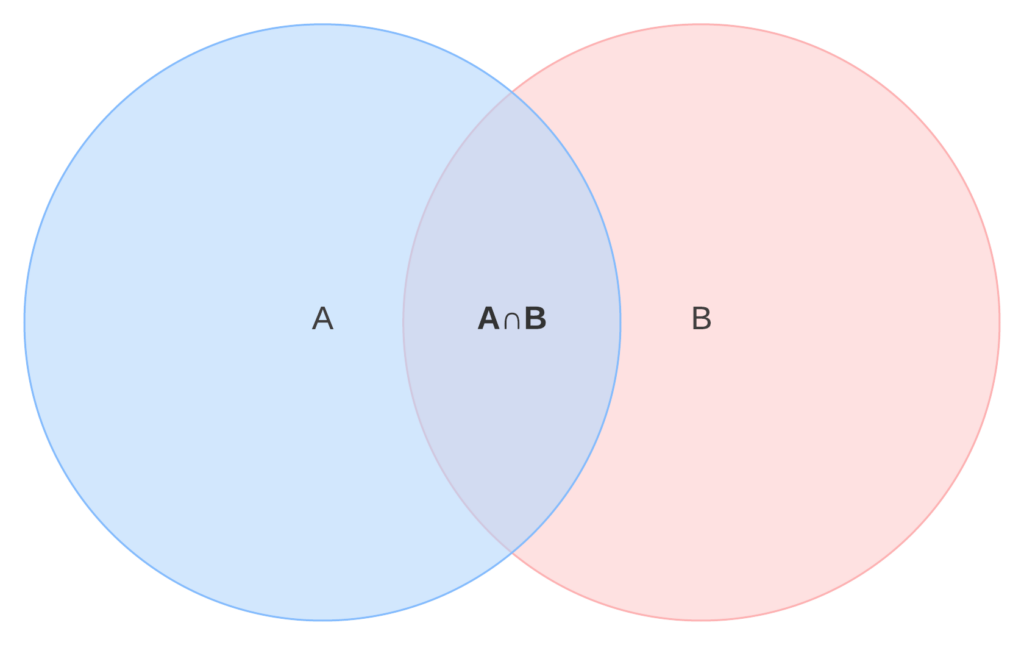
En segundo lugar, es importante entender lo que es la intersección de conjuntos. La intersección de dos conjuntos A y B se define como el conjunto de elementos que pertenecen tanto a A como a B. Esto se representa mediante la superposición de los círculos o elipses correspondientes, como se muestra en la siguiente figura:

En tercer lugar, es importante entender lo que es la unión de conjuntos. La unión de dos conjuntos A y B se define como el conjunto de elementos que pertenecen a A o a B. Esto se representa mediante la superposición de los círculos o elipses correspondientes, como se muestra en la siguiente figura:

¿Cómo se aplican los diagramas de Venn en la teoría de conjuntos?
Los diagramas de Venn se pueden utilizar para resolver problemas de teoría de conjuntos. Por ejemplo, supongamos que tenemos dos conjuntos A y B, y queremos encontrar la intersección entre ellos. Podemos representar los conjuntos A y B mediante círculos o elipses, y luego superponerlos para encontrar la intersección, como se muestra en la siguiente figura:

De esta manera, podemos visualizar fácilmente la intersección entre A y B, que es el conjunto de elementos que pertenecen tanto a A como a B.
¿Cómo se pueden utilizar los diagramas de Venn en otras áreas de las matemáticas?
Los diagramas de Venn no solo se utilizan en la teoría de conjuntos, sino que también se pueden utilizar en otras áreas de las matemáticas. Por ejemplo, los diagramas de Venn se pueden utilizar para representar los números primos y los números compuestos. En este caso, los círculos o elipses representan los números primos y los números compuestos, y la superposición de los círculos o elipses representa los números que son tanto primos como compuestos.
Conclusión
La representación visual de la teoría de conjuntos es una herramienta poderosa que nos permite entender mejor los conceptos fundamentales de esta teoría. Los diagramas de Venn son una forma común de representar los conjuntos y sus relaciones de una manera visual. La inclusión de conjuntos, la intersección de conjuntos y la unión de conjuntos se pueden representar fácilmente mediante diagramas de Venn. Los diagramas de Venn también se pueden utilizar en otras áreas de las matemáticas, como la representación de los números primos y compuestos.
Preguntas frecuentes
1. ¿Qué es la teoría de conjuntos?
La teoría de conjuntos es una rama de las matemáticas que se ocupa del estudio de los conjuntos, que son colecciones de objetos.
2. ¿Qué son los diagramas de Venn?
Los diagramas de Venn son una forma común de representar los conjuntos y sus relaciones de una manera visual.
3. ¿Cómo se pueden utilizar los diagramas de Venn en la teoría de conjuntos?
Los diagramas de Venn se pueden utilizar para resolver problemas de teoría de conjuntos, como encontrar la intersección entre dos conjuntos.
4. ¿Cómo se pueden utilizar los diagramas de Venn en otras áreas de las matemáticas?
Los diagramas de Venn se pueden utilizar en otras áreas de las matemáticas, como la representación de los números primos y compuestos.
5. ¿Por qué son útiles los diagramas de Venn?
Los diagramas de Venn son útiles porque permiten representar visualmente los conjuntos y sus relaciones, lo que facilita la comprensión de los conceptos fundamentales de la teoría de conjuntos.
Deja una respuesta