Descubre la lógica tras los circuitos con álgebra booleana y conjuntos

Los circuitos electrónicos están presentes en muchos aspectos de nuestra vida diaria, desde los dispositivos móviles que usamos hasta los sistemas de seguridad que protegen nuestras casas. Pero, ¿alguna vez te has preguntado cómo funcionan realmente? La respuesta se encuentra en la lógica detrás de los circuitos, que se puede analizar y comprender mediante el uso del álgebra booleana y los conjuntos.

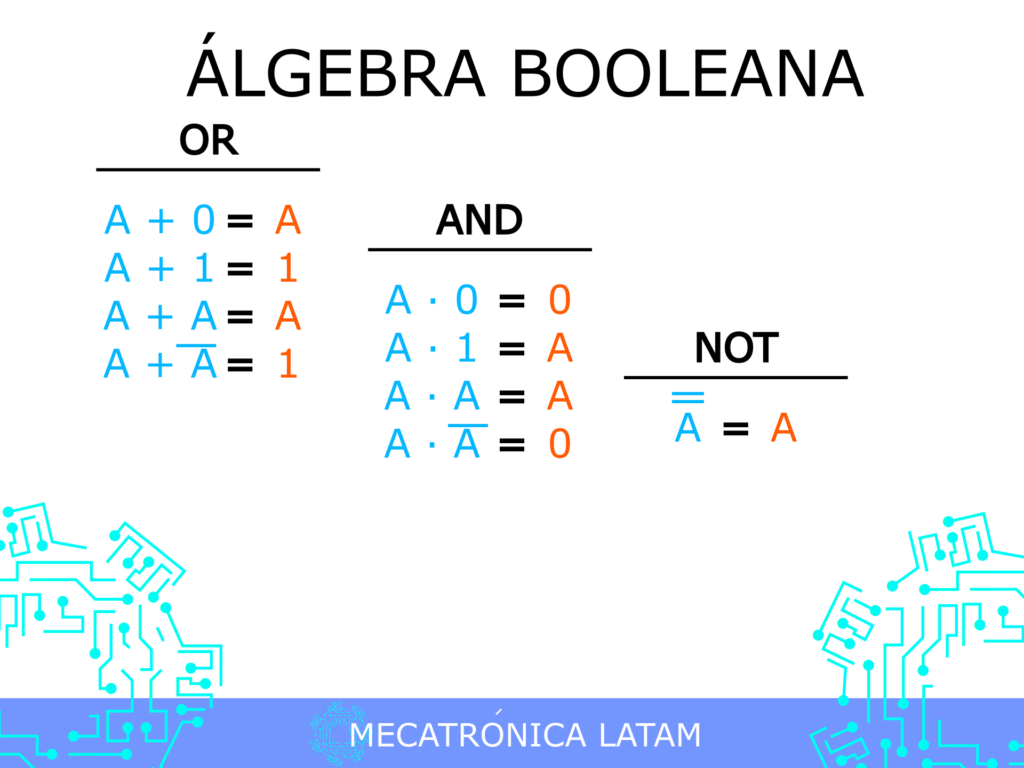
¿Qué es el álgebra booleana?

El álgebra booleana es una rama de las matemáticas que se enfoca en el estudio de las operaciones lógicas y las funciones booleanas. Una función booleana es una expresión matemática que toma una o más variables booleanas (que solo pueden tener dos valores posibles: verdadero o falso) y produce un resultado booleano.

En los circuitos electrónicos, las variables booleanas corresponden a los estados de los componentes electrónicos, como interruptores o transistores. Mediante la combinación de estas variables y el uso de operaciones lógicas como la negación, la conjunción y la disyunción, se pueden crear circuitos complejos que realizan tareas específicas.

¿Cómo se relaciona el álgebra booleana con los circuitos electrónicos?

Los circuitos electrónicos se pueden representar mediante diagramas de circuitos que muestran los componentes y las conexiones entre ellos. Estos diagramas se pueden analizar utilizando álgebra booleana para determinar cómo se comportará el circuito en diferentes situaciones.

Por ejemplo, consideremos un circuito simple que consta de dos interruptores conectados en serie. Si ambos interruptores están cerrados, la corriente eléctrica puede fluir a través del circuito y encender una luz conectada al final del mismo. Sin embargo, si uno de los interruptores se abre, la corriente se interrumpe y la luz se apaga.

Este circuito se puede representar mediante una función booleana que toma dos variables booleanas (una para cada interruptor) y produce un resultado booleano que indica si la luz está encendida o apagada. Mediante el uso de la operación lógica de conjunción (AND), podemos combinar las variables booleanas para modelar el comportamiento del circuito.

¿Qué son los conjuntos?

Los conjuntos son una herramienta matemática que se utiliza para representar colecciones de objetos. Cada objeto en un conjunto se llama elemento, y los conjuntos se pueden combinar mediante operaciones como la unión, la intersección y la diferencia.

En el contexto de los circuitos electrónicos, los conjuntos se utilizan para representar los estados de los componentes electrónicos. Por ejemplo, podemos tener un conjunto que representa los estados posibles de un interruptor (abierto o cerrado), o un conjunto que representa los estados posibles de un transistor (encendido o apagado).

¿Cómo se relacionan los conjuntos con el álgebra booleana?

Los conjuntos y el álgebra booleana están estrechamente relacionados, ya que las operaciones lógicas se pueden interpretar como operaciones sobre conjuntos. Por ejemplo, la operación lógica de conjunción (AND) se puede interpretar como una intersección de conjuntos, mientras que la operación de disyunción (OR) se puede interpretar como una unión de conjuntos.

Además, los conjuntos se pueden utilizar para simplificar las expresiones booleanas y hacer que su análisis sea más fácil. Por ejemplo, podemos representar una función booleana mediante un conjunto de elementos que producen un resultado verdadero, y luego utilizar operaciones de conjunto para simplificar la expresión y eliminar términos redundantes.

Conclusión

El álgebra booleana y los conjuntos son herramientas esenciales para el análisis de circuitos electrónicos. Mediante el uso de estas herramientas, podemos entender cómo funcionan los circuitos y crear diseños complejos que realizan tareas específicas. Por lo tanto, si estás interesado en la electrónica, es importante que te familiarices con estas herramientas y las utilices en tus proyectos.

Preguntas frecuentes

1. ¿Qué es una función booleana?

Una función booleana es una expresión matemática que toma una o más variables booleanas y produce un resultado booleano. Las variables booleanas solo pueden tener dos valores posibles: verdadero o falso.

2. ¿Qué son las operaciones lógicas?

Las operaciones lógicas son operaciones que se utilizan para combinar variables booleanas y producir un resultado booleano. Algunas operaciones lógicas comunes son la negación, la conjunción y la disyunción.

3. ¿Cómo se utilizan los conjuntos en los circuitos electrónicos?

Los conjuntos se utilizan para representar los estados posibles de los componentes electrónicos, como interruptores o transistores. Los conjuntos se pueden combinar mediante operaciones de conjunto para simplificar las expresiones booleanas y hacer que su análisis sea más fácil.

4. ¿Qué es un circuito electrónico?

Un circuito electrónico es un conjunto de componentes electrónicos interconectados que realizan una función específica. Los circuitos electrónicos se pueden encontrar en una amplia variedad de dispositivos, desde teléfonos móviles hasta sistemas de seguridad.

5. ¿Por qué es importante entender el álgebra booleana y los conjuntos en la electrónica?

El álgebra booleana y los conjuntos son herramientas esenciales para el análisis de circuitos electrónicos. Al entender estas herramientas, podemos diseñar circuitos más efectivos y realizar tareas más complejas. Además, el conocimiento del álgebra booleana y los conjuntos es esencial para cualquier persona que esté interesada en la electrónica y quiera trabajar en este campo.