Descubre la lógica simbólica: definición y ejemplos

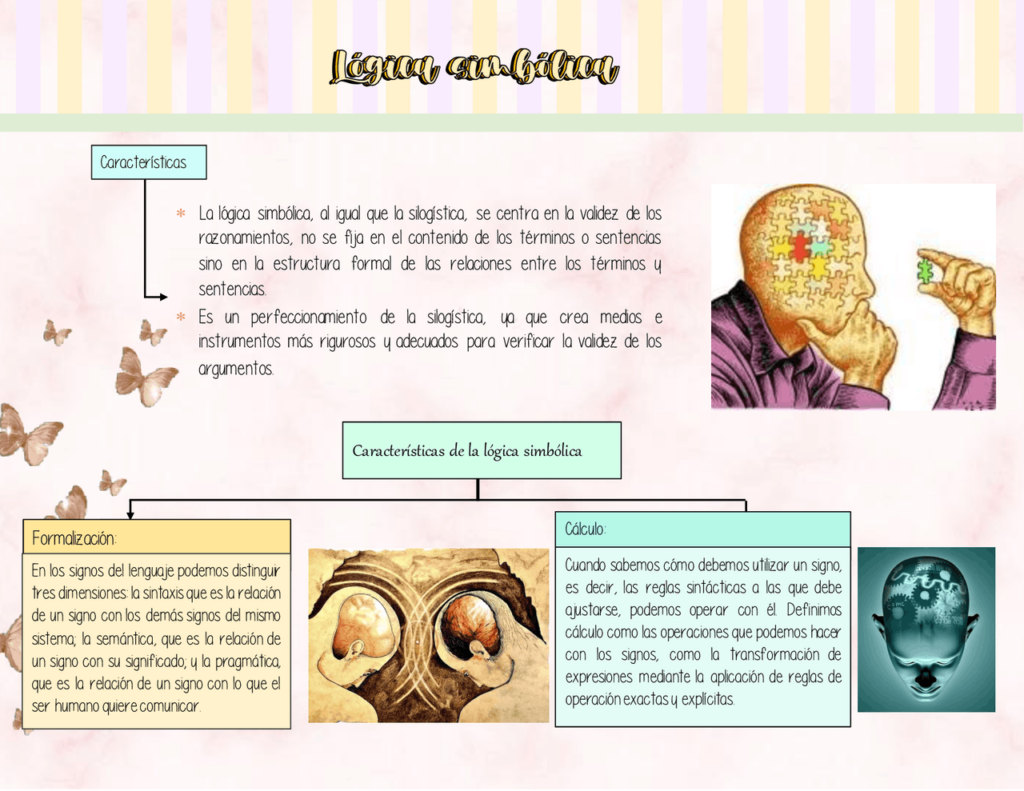
La lógica simbólica es una rama de la filosofía que se encarga de estudiar el razonamiento y las relaciones entre los conceptos. Esta disciplina utiliza símbolos para representar los conceptos y las proposiciones y así poder analizarlos de manera más precisa. En este artículo, te explicaremos en qué consiste la lógica simbólica y te mostraremos algunos ejemplos para que puedas entender mejor su funcionamiento.

¿Qué es la lógica simbólica?

La lógica simbólica es una herramienta que se utiliza para analizar y evaluar los argumentos de manera rigurosa y sistemática. Su objetivo principal es establecer la validez o invalidez de un argumento, es decir, determinar si las conclusiones que se derivan de las premisas son verdaderas o falsas.

En la lógica simbólica, los conceptos se representan mediante símbolos que permiten analizarlos de manera más precisa. Estos símbolos pueden ser letras, números o signos especiales, y se utilizan para representar tanto los conceptos como las proposiciones.

Ejemplos de lógica simbólica

A continuación, te mostraremos algunos ejemplos de lógica simbólica para que puedas entender mejor cómo funciona esta disciplina:

Ejemplo 1:

Premisa 1: Todos los gatos son animales.
Premisa 2: El gato de Ana es un gato.
Conclusión: El gato de Ana es un animal.

En este ejemplo, los símbolos utilizados para representar los conceptos son "gato" y "animal". Las premisas se representan mediante las letras P1 y P2, y la conclusión se representa mediante la letra C.

Ejemplo 2:

Premisa 1: Si llueve, el suelo estará mojado.
Premisa 2: Está lloviendo.
Conclusión: El suelo está mojado.

En este ejemplo, los símbolos utilizados representan los conceptos "llueve" y "el suelo está mojado". Las premisas se representan mediante las letras P1 y P2, y la conclusión se representa mediante la letra C.

¿Cómo se utiliza la lógica simbólica?

Para utilizar la lógica simbólica, es necesario seguir un conjunto de reglas y convenciones que permiten analizar los argumentos de manera rigurosa y sistemática. Estas reglas y convenciones incluyen:

- La utilización de símbolos para representar los conceptos y las proposiciones.
- La utilización de conectores lógicos, como "y", "o", "si...entonces", para unir las proposiciones.
- La utilización de reglas de inferencia para derivar conclusiones a partir de las premisas.

Beneficios de la lógica simbólica

La lógica simbólica tiene varios beneficios, entre los que se incluyen:

- Ayuda a mejorar la capacidad de análisis y razonamiento.
- Permite analizar de manera rigurosa y sistemática los argumentos.
- Facilita la identificación de errores en los argumentos.
- Ayuda a desarrollar habilidades de resolución de problemas.

Conclusión

La lógica simbólica es una herramienta muy útil para analizar y evaluar los argumentos de manera rigurosa y sistemática. Esta disciplina utiliza símbolos para representar los conceptos y las proposiciones, lo que permite analizarlos de manera más precisa. Además, la lógica simbólica tiene varios beneficios, entre los que se incluyen la mejora de la capacidad de análisis y razonamiento, la identificación de errores en los argumentos y el desarrollo de habilidades de resolución de problemas.

Preguntas frecuentes

1. ¿La lógica simbólica solo se utiliza en filosofía?

No, la lógica simbólica se utiliza en diversas disciplinas, como las matemáticas, la informática y la inteligencia artificial.

2. ¿Es necesario conocer las reglas de la lógica simbólica para utilizarla?

Sí, es necesario conocer las reglas y convenciones de la lógica simbólica para utilizarla de manera efectiva.

3. ¿La lógica simbólica solo se utiliza para analizar argumentos deductivos?

No, la lógica simbólica también se utiliza para analizar argumentos inductivos y abductivos.

4. ¿Qué es un argumento deductivo?

Un argumento deductivo es aquel en el que la conclusión se deduce necesariamente de las premisas. Es decir, si las premisas son verdaderas, la conclusión también lo será.

5. ¿Qué es un argumento inductivo?

Un argumento inductivo es aquel en el que la conclusión se infiere a partir de la observación de casos particulares. En este tipo de argumento, la conclusión no se deduce necesariamente de las premisas, sino que se basa en la probabilidad.