Descubre la lógica proposicional con operadores lógicos
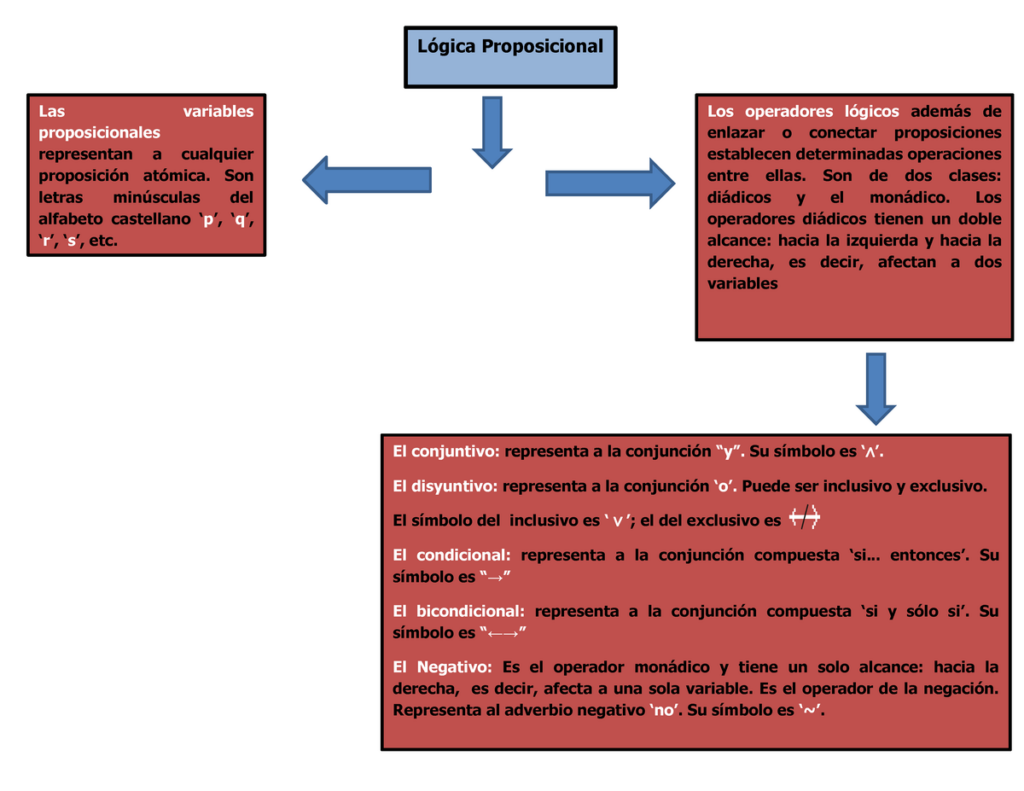
La lógica proposicional es una rama de la lógica que se enfoca en el estudio de proposiciones o afirmaciones. Las proposiciones son declaraciones que pueden ser verdaderas o falsas, y se representan mediante letras o símbolos para facilitar su análisis.
Los operadores lógicos son herramientas fundamentales en la lógica proposicional, ya que permiten la construcción de proposiciones más complejas a partir de proposiciones simples. En este artículo, descubriremos qué son los operadores lógicos y cómo se utilizan en la lógica proposicional.
¿Qué son los operadores lógicos?
Los operadores lógicos son símbolos que permiten combinar proposiciones simples para formar proposiciones más complejas. Estos operadores se utilizan en la lógica proposicional para evaluar la verdad o falsedad de una proposición a partir de la verdad o falsedad de sus componentes.
Existen tres operadores lógicos fundamentales en la lógica proposicional: la negación, la conjunción y la disyunción.
La negación
El operador de negación se representa con el símbolo ¬ y se utiliza para cambiar el valor de verdad de una proposición. Por ejemplo, si la proposición "El cielo está azul" es verdadera, entonces la proposición "El cielo no está azul" será falsa.
La conjunción
El operador de conjunción se representa con el símbolo ∧ y se utiliza para combinar dos proposiciones simples en una sola proposición. La proposición resultante será verdadera solo si ambas proposiciones simples son verdaderas. Por ejemplo, si la proposición "Hoy es domingo" es verdadera y la proposición "Hace sol" es verdadera, entonces la proposición "Hoy es domingo y hace sol" también será verdadera.
La disyunción
El operador de disyunción se representa con el símbolo ∨ y se utiliza para combinar dos proposiciones simples en una sola proposición. La proposición resultante será verdadera si al menos una de las proposiciones simples es verdadera. Por ejemplo, si la proposición "Hoy es domingo" es verdadera y la proposición "Hace frío" es falsa, entonces la proposición "Hoy es domingo o hace frío" será verdadera.
Ejemplos de uso de los operadores lógicos
A continuación, presentamos algunos ejemplos de cómo se utilizan los operadores lógicos en la lógica proposicional:
Ejemplo 1
Supongamos que tenemos las siguientes proposiciones simples:
A: "Mi perro es blanco"
B: "Mi perro ladra mucho"
La proposición "Mi perro es blanco y ladra mucho" se puede representar utilizando el operador de conjunción ∧ de la siguiente manera:
A ∧ B
Esta proposición será verdadera solo si ambas proposiciones simples son verdaderas.
Ejemplo 2
Supongamos que tenemos las siguientes proposiciones simples:
C: "Hoy es lunes"
D: "Mañana es martes"
La proposición "Hoy no es lunes o mañana es martes" se puede representar utilizando el operador de disyunción ∨ y el operador de negación ¬ de la siguiente manera:
¬C ∨ D
Esta proposición será verdadera si hoy no es lunes o si mañana es martes.
Conclusión
Los operadores lógicos son herramientas fundamentales en la lógica proposicional, ya que permiten la construcción de proposiciones más complejas a partir de proposiciones simples. La negación, la conjunción y la disyunción son los operadores lógicos fundamentales en la lógica proposicional.
Preguntas frecuentes
1. ¿Existen otros operadores lógicos?
Sí, existen otros operadores lógicos en la lógica proposicional, como la implicación y la equivalencia. Estos operadores son utilizados para construir proposiciones más complejas y se representan con los símbolos → y ↔, respectivamente.
2. ¿Qué es una proposición?
Una proposición es una declaración que puede ser verdadera o falsa. Por ejemplo, "Hoy es lunes" es una proposición, mientras que "¿Qué hora es?" no lo es.
3. ¿Cómo se evalúa la verdad o falsedad de una proposición compleja?
La verdad o falsedad de una proposición compleja se evalúa a partir de la verdad o falsedad de sus componentes utilizando los operadores lógicos correspondientes.
4. ¿Qué es una tautología?
Una tautología es una proposición que siempre es verdadera, independientemente de los valores de verdad de sus componentes. Por ejemplo, la proposición "El cielo es azul o no lo es" es una tautología, ya que siempre será verdadera.
5. ¿Qué es una contradicción?
Una contradicción es una proposición que siempre es falsa, independientemente de los valores de verdad de sus componentes. Por ejemplo, la proposición "El cielo es azul y no es azul" es una contradicción, ya que siempre será falsa.
Deja una respuesta