Descubre la lógica matemática: mapa conceptual
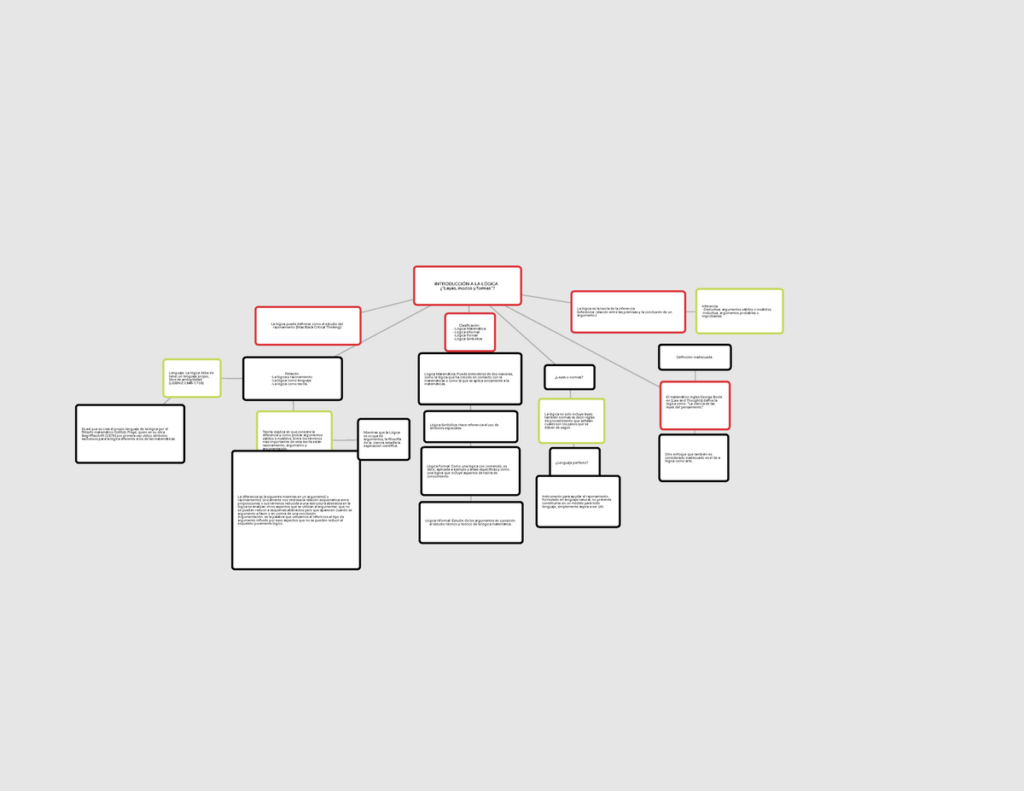
La lógica matemática es una rama de la matemática que se encarga de estudiar los principios y métodos que se utilizan para razonar correctamente. Esta disciplina es fundamental en diversas áreas del conocimiento, desde la filosofía hasta la ciencia de la computación. En este artículo, te presentaremos un mapa conceptual de la lógica matemática para que puedas entender mejor sus conceptos y aplicaciones.
¿Qué es la lógica matemática?
La lógica matemática es una rama de la matemática que se encarga del estudio de la inferencia, la demostración y la verificación de los argumentos. Esta disciplina utiliza símbolos y reglas formales para representar y manipular los razonamientos en un lenguaje claro y preciso. La lógica matemática tiene sus raíces en la filosofía, pero hoy en día es una herramienta fundamental en la matemática, la informática, la inteligencia artificial y otras disciplinas.
Los elementos de la lógica matemática
La lógica matemática se divide en dos partes principales: la sintaxis y la semántica. La sintaxis se refiere a la estructura formal del lenguaje utilizado en la lógica matemática, mientras que la semántica se refiere a su significado.
La sintaxis de la lógica matemática
La sintaxis de la lógica matemática se basa en el uso de símbolos y reglas formales para representar los razonamientos. Los símbolos más comunes en la lógica matemática son los siguientes:
- Conectivos lógicos: AND, OR, NOT, IF-THEN, IF AND ONLY IF.
- Variables proposicionales: p, q, r, s, etc.
- Constantes proposicionales: verdadero (T) y falso (F).
- Cuantificadores: para todo (∀) y existe (∃).
- Símbolos de igualdad: =.
Estos símbolos se utilizan para construir fórmulas lógicas que representan los razonamientos. Estas fórmulas se construyen utilizando las siguientes reglas formales:
- Las variables proposicionales representan afirmaciones o proposiciones.
- Los conectivos lógicos combinan proposiciones para formar nuevas proposiciones.
- Los cuantificadores permiten cuantificar sobre el universo de discurso.
- Las fórmulas lógicas se pueden construir mediante la aplicación de reglas formales.
La semántica de la lógica matemática
La semántica de la lógica matemática se refiere al significado de las fórmulas lógicas. Para dar un significado a las fórmulas lógicas, se utilizan modelos. Un modelo es una interpretación de las variables proposicionales y los conectivos lógicos dentro de un contexto particular.
Un modelo se define por una función de interpretación que asigna un valor de verdad (verdadero o falso) a cada variable proposicional y una interpretación de los conectivos lógicos. Por ejemplo, si p representa la proposición "El cielo es azul" y q representa la proposición "El sol brilla", un modelo podría asignar el valor verdadero a p y el valor falso a q.
Una vez que se ha definido un modelo, se puede determinar el valor de verdad de cualquier fórmula lógica en ese modelo. Una fórmula lógica es verdadera en un modelo si su valor de verdad es verdadero para todas las interpretaciones posibles.
Las aplicaciones de la lógica matemática
La lógica matemática tiene muchas aplicaciones en diversos campos del conocimiento. Algunas de las aplicaciones más importantes son las siguientes:
- La matemática: la lógica matemática es fundamental para la construcción y la verificación de las demostraciones matemáticas.
- La filosofía: la lógica matemática es una herramienta importante en la filosofía para el análisis crítico de los argumentos.
- La informática: la lógica matemática es esencial para la programación de ordenadores y la creación de algoritmos.
- La inteligencia artificial: la lógica matemática se utiliza en la creación de sistemas inteligentes y la toma de decisiones automatizada.
Conclusión
La lógica matemática es una disciplina fundamental en la matemática, la filosofía, la informática y la inteligencia artificial. Su sintaxis se basa en el uso de símbolos y reglas formales para representar y manipular los razonamientos, mientras que su semántica se refiere al significado de las fórmulas lógicas en un contexto particular. Esperamos que este mapa conceptual te haya ayudado a entender mejor los conceptos y aplicaciones de la lógica matemática.
Preguntas frecuentes
¿Qué es un modelo en lógica matemática?
Un modelo en lógica matemática es una interpretación de las variables proposicionales y los conectivos lógicos dentro de un contexto particular.
¿Qué es un cuantificador en lógica matemática?
Un cuantificador en lógica matemática es un símbolo que permite cuantificar sobre el universo de discurso. Los cuantificadores más comunes son "para todo" (∀) y "existe" (∃).
¿Qué aplicaciones tiene la lógica matemática?
La lógica matemática tiene aplicaciones en la matemática, la filosofía, la informática y la inteligencia artificial.
¿Qué es la sintaxis en lógica matemática?
La sintaxis en lógica matemática se refiere a la estructura formal del lenguaje utilizado en la lógica matemática. Se basa en el uso de símbolos y reglas formales para representar los razonamientos.
¿Qué es la semántica en lógica matemática?
La semántica en lógica matemática se refiere al significado de las fórmulas lógicas. Se utiliza para dar un significado a las fórmulas lógicas mediante la definición de modelos.
Deja una respuesta