Descubre la lógica matemática: ejemplos de proposiciones simples y compuestas
La lógica matemática es una rama de las matemáticas que se ocupa del estudio de la verdad y la falsedad de las proposiciones. En la lógica matemática, una proposición es cualquier afirmación que puede ser verdadera o falsa. Las proposiciones se pueden clasificar en simples y compuestas.
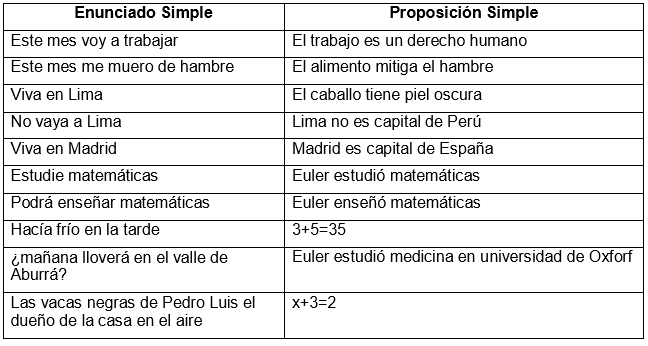
Las proposiciones simples son aquellas que no se pueden dividir en partes más pequeñas. Por ejemplo, "El cielo es azul" es una proposición simple, ya que no se puede dividir en partes más pequeñas. Otras proposiciones simples comunes son "2 + 2 = 4" y "La Tierra gira alrededor del Sol".
Las proposiciones compuestas son aquellas que se construyen a partir de proposiciones simples utilizando conectivos lógicos como "y", "o" y "no". Por ejemplo, "El cielo es azul y el sol es amarillo" es una proposición compuesta, ya que se construye a partir de dos proposiciones simples unidas por el conectivo "y". Otras proposiciones compuestas comunes son "Si llueve, entonces me quedo en casa" y "El número es par o es múltiplo de 3".
Es importante tener en cuenta que las proposiciones compuestas también pueden ser verdaderas o falsas. La verdad o falsedad de una proposición compuesta depende de la verdad o falsedad de sus proposiciones simples y de la forma en que están conectadas por los conectivos lógicos.
Aquí hay algunos ejemplos de proposiciones simples y compuestas:
Proposiciones simples:
- 2 + 2 = 4
- El agua hierve a 100 grados Celsius
- La luna es un satélite natural de la Tierra
Proposiciones compuestas:
- Si estudio, entonces sacaré buenas notas
- El gato es negro o el perro es marrón
- No es cierto que la Tierra sea plana
Es importante tener en cuenta que los conectivos lógicos pueden cambiar el significado de una proposición. Por ejemplo, "El gato es negro o el perro es marrón" es verdadero si el gato es negro, si el perro es marrón, o si ambos son ciertos. Sin embargo, "El gato es negro y el perro es marrón" solo es verdadero si ambas proposiciones son ciertas.
La lógica matemática es una herramienta importante para entender la verdad y la falsedad de las proposiciones. Las proposiciones simples son aquellas que no se pueden dividir en partes más pequeñas, mientras que las proposiciones compuestas se construyen a partir de proposiciones simples utilizando conectivos lógicos. Es importante entender que los conectivos lógicos pueden cambiar el significado de una proposición y que la verdad o falsedad de una proposición compuesta depende de la verdad o falsedad de sus proposiciones simples y de la forma en que están conectadas.
Preguntas frecuentes
¿Qué es una proposición en lógica matemática?
Una proposición es cualquier afirmación que puede ser verdadera o falsa.
¿Cuál es la diferencia entre una proposición simple y una compuesta?
Las proposiciones simples son aquellas que no se pueden dividir en partes más pequeñas, mientras que las proposiciones compuestas se construyen a partir de proposiciones simples utilizando conectivos lógicos.
¿Qué son los conectivos lógicos?
Los conectivos lógicos son palabras o símbolos que se utilizan para unir proposiciones simples y formar proposiciones compuestas. Algunos ejemplos comunes de conectivos lógicos son "y", "o" y "no".
¿Cómo se determina la verdad o falsedad de una proposición compuesta?
La verdad o falsedad de una proposición compuesta depende de la verdad o falsedad de sus proposiciones simples y de la forma en que están conectadas por los conectivos lógicos.
¿Por qué es importante entender la lógica matemática?
La lógica matemática es una herramienta importante para entender la verdad y la falsedad de las afirmaciones. Además, la lógica matemática se utiliza en muchos campos, incluyendo la informática, la filosofía y las ciencias naturales.
Deja una respuesta