Descubre la lógica matemática con ejemplos de proposiciones
La lógica matemática es una rama de las matemáticas que se centra en el estudio de la deducción y el razonamiento. En la lógica matemática, se utilizan proposiciones para analizar y demostrar teoremas y argumentos. En este artículo, exploraremos la lógica matemática a través de ejemplos de proposiciones.
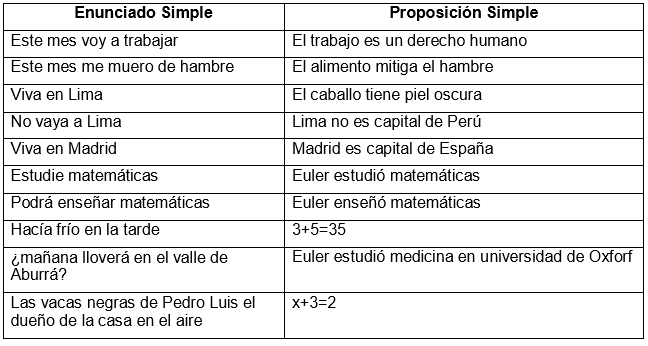
¿Qué es una proposición?
Una proposición es una afirmación que puede ser verdadera o falsa, pero no ambas cosas a la vez. Por ejemplo, "2 + 2 = 4" es una proposición verdadera, mientras que "el cielo es verde" es una proposición falsa.
Conectores lógicos
Los conectores lógicos son palabras o símbolos que se utilizan para unir proposiciones y formar nuevas proposiciones. Los conectores más comunes son:
- Conjunción: se utiliza para unir dos proposiciones con la palabra "y" o el símbolo "^". Por ejemplo, "2 + 2 = 4 y 3 + 3 = 6" es una proposición compuesta que une dos proposiciones verdaderas.
- Disyunción: se utiliza para unir dos proposiciones con la palabra "o" o el símbolo "v". Por ejemplo, "el sol es amarillo o el cielo es azul" es una proposición compuesta que une dos proposiciones verdaderas.
- Negación: se utiliza para negar una proposición con la palabra "no" o el símbolo "~". Por ejemplo, "no es cierto que 1 + 1 = 3" es una proposición negada.
- Implicación: se utiliza para expresar una relación de causa y efecto con la palabra "si...entonces" o el símbolo "→". Por ejemplo, "si llueve, entonces me quedo en casa" es una proposición compuesta que une dos proposiciones verdaderas.
Ejemplos de proposiciones
Veamos algunos ejemplos de proposiciones y cómo se pueden combinar para formar proposiciones compuestas.
- Proposición simple: "El agua hierve a 100°C".
- Proposición simple: "Los gatos tienen cuatro patas".
- Proposición compuesta: "El agua hierve a 100°C y los gatos tienen cuatro patas".
- Proposición simple: "Los pájaros vuelan".
- Proposición simple: "Los pingüinos no vuelan".
- Proposición compuesta: "Los pájaros vuelan o los pingüinos no vuelan".
- Proposición simple: "El sol sale todas las mañanas".
- Proposición negada: "No es cierto que el sol salga todas las mañanas".
- Proposición compuesta: "Si llueve, entonces me quedo en casa".
Tablas de verdad
Las tablas de verdad son una herramienta útil para analizar proposiciones compuestas y determinar su valor de verdad en función de los valores de verdad de las proposiciones simples que las componen. Veamos un ejemplo de tabla de verdad para la proposición "p y q":
| p | q | p y q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
La tabla muestra los diferentes valores de verdad para la proposición compuesta "p y q" en función de los valores de verdad de las proposiciones simples "p" y "q".
Conclusión
La lógica matemática es una herramienta útil para analizar y demostrar argumentos y teoremas. Las proposiciones son la base de la lógica matemática y se pueden combinar con conectores lógicos para formar proposiciones compuestas. Las tablas de verdad son una herramienta útil para analizar proposiciones compuestas y determinar su valor de verdad.
Preguntas frecuentes
¿Qué es una proposición?
Una proposición es una afirmación que puede ser verdadera o falsa, pero no ambas cosas a la vez.
¿Cuáles son los conectores lógicos?
Los conectores lógicos más comunes son la conjunción, la disyunción, la negación y la implicación.
¿Cómo se combinan las proposiciones para formar proposiciones compuestas?
Las proposiciones se combinan con conectores lógicos para formar proposiciones compuestas.
¿Qué son las tablas de verdad?
Las tablas de verdad son una herramienta útil para analizar proposiciones compuestas y determinar su valor de verdad en función de los valores de verdad de las proposiciones simples que las componen.
¿Por qué es importante la lógica matemática?
La lógica matemática es una herramienta útil para analizar y demostrar argumentos y teoremas de manera rigurosa y precisa. Además, es una herramienta esencial en disciplinas como la informática y la filosofía.
Deja una respuesta