Descubre la lógica formal y su principio de identidad
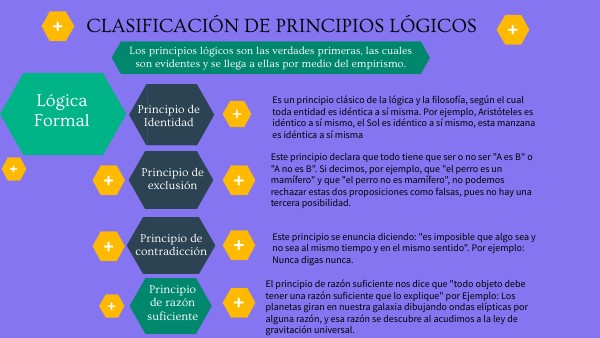
La lógica formal es una disciplina que se encarga de estudiar las reglas y principios que rigen el razonamiento humano. En otras palabras, se trata de un conjunto de herramientas que nos permiten analizar y evaluar argumentos de forma rigurosa y sistemática. Uno de los principios fundamentales de la lógica formal es el principio de identidad, que establece que una cosa es idéntica a sí misma.
En este artículo, te invitamos a descubrir más sobre este principio y su importancia en la lógica formal.
¿Qué es el principio de identidad?
El principio de identidad es uno de los principios fundamentales de la lógica formal. Se trata de una afirmación que establece que una cosa es idéntica a sí misma. En otras palabras, si decimos que algo es A, entonces ese algo siempre será A y no B o C. Este principio es muy importante en la lógica formal, ya que nos permite establecer relaciones de igualdad entre diferentes cosas.
¿Cómo se aplica el principio de identidad?
El principio de identidad se aplica en diferentes ámbitos de la lógica formal. Por ejemplo, en la lógica proposicional, se utiliza para evaluar la verdad o falsedad de una proposición. Si decimos que "el cielo es azul", entonces esa proposición siempre será verdadera en tanto que se refiere a las características del cielo. Si decimos que "el cielo es verde", entonces esa proposición será falsa, porque va en contra de la realidad observada.
En la lógica de predicados, el principio de identidad se utiliza para establecer la identidad entre diferentes objetos. Por ejemplo, si decimos que "Juan es el padre de Pedro", entonces estamos estableciendo una relación entre dos objetos diferentes: Juan y Pedro. Sin embargo, el principio de identidad nos permite afirmar que Juan es siempre Juan y Pedro es siempre Pedro, y que esta relación entre ellos es única y no puede ser confundida con otra.
¿Por qué es importante el principio de identidad?
El principio de identidad es importante en la lógica formal porque nos permite establecer relaciones de igualdad entre diferentes cosas. Gracias a este principio, podemos analizar y evaluar argumentos de forma rigurosa y sistemática, y establecer la verdad o falsedad de las proposiciones que se nos presentan.
Además, el principio de identidad es esencial en muchas áreas del conocimiento, como la matemática, la física o la filosofía. En la matemática, por ejemplo, el principio de identidad es la base de la teoría de conjuntos, que establece las reglas para la formación de conjuntos y las operaciones que se pueden realizar con ellos. En la física, el principio de identidad se utiliza para establecer la continuidad de los procesos físicos a lo largo del tiempo. En la filosofía, el principio de identidad es un tema central en la discusión sobre la identidad personal y la persistencia a lo largo del tiempo.
Ejemplos de aplicación del principio de identidad
Para ilustrar la aplicación del principio de identidad, vamos a ver algunos ejemplos concretos:
- Si decimos que "el perro es un animal", entonces estamos estableciendo una relación de identidad entre el perro y el conjunto de los animales. El perro sigue siendo siempre el perro, pero ahora sabemos que pertenece al conjunto de los animales.
- Si decimos que "la suma de dos más dos es igual a cuatro", entonces estamos aplicando el principio de identidad a las operaciones matemáticas. La suma de dos más dos siempre será igual a cuatro, y no a otro número.
- Si decimos que "la luz se propaga en línea recta", entonces estamos aplicando el principio de identidad a las leyes de la física. La luz siempre se propaga en línea recta, y no en otra dirección.
Conclusión
El principio de identidad es uno de los principios fundamentales de la lógica formal. Este principio establece que una cosa es idéntica a sí misma, y nos permite establecer relaciones de igualdad entre diferentes cosas. Gracias a este principio, podemos analizar y evaluar argumentos de forma rigurosa y sistemática, y establecer la verdad o falsedad de las proposiciones que se nos presentan.
Preguntas frecuentes
1. ¿Qué otros principios fundamentales existen en la lógica formal?
Además del principio de identidad, existen otros principios fundamentales en la lógica formal, como el principio de no contradicción y el principio del tercero excluido.
2. ¿Cómo se utiliza el principio de identidad en la teoría de conjuntos?
En la teoría de conjuntos, el principio de identidad se utiliza para establecer las reglas para la formación de conjuntos y las operaciones que se pueden realizar con ellos.
3. ¿Por qué es importante el principio de identidad en la filosofía?
El principio de identidad es importante en la filosofía porque es un tema central en la discusión sobre la identidad personal y la persistencia a lo largo del tiempo.
4. ¿Cómo se aplica el principio de identidad en la física?
En física, el principio de identidad se utiliza para establecer la continuidad de los procesos físicos a lo largo del tiempo.
5. ¿Qué otros ámbitos del conocimiento utilizan el principio de identidad?
Además de la lógica, la matemática y la física, el principio de identidad es utilizado en muchos otros ámbitos del conocimiento, como la biología, la química o la informática.
Deja una respuesta