Descubre la lógica detrás del triángulo en la proposición

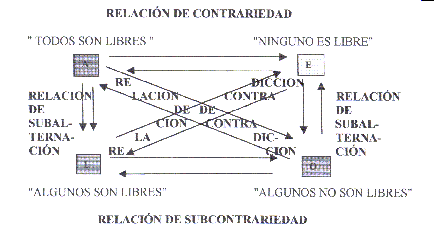
Si has estudiado lógica, es probable que hayas visto el triángulo en la proposición en algún momento. Este símbolo es utilizado para representar una implicación o condicional entre dos proposiciones. En este artículo, exploraremos la lógica detrás del triángulo en la proposición y cómo se utiliza en la teoría de la lógica.

¿Qué es una proposición?

Antes de hablar sobre el triángulo en la proposición, es importante entender qué es una proposición en sí misma. Una proposición es una afirmación que puede ser verdadera o falsa. Por ejemplo, "el cielo es azul" es una proposición, mientras que "mi gato es bonito" no lo es, ya que es una cuestión de opinión personal.

Las proposiciones se utilizan en la lógica para construir argumentos y razonamientos. Los argumentos constan de una o más proposiciones y se usan para llegar a una conclusión.

¿Qué es una implicación o condicional?

Una implicación o condicional es una proposición que establece una relación entre dos proposiciones. La implicación se lee como "si A, entonces B". Por ejemplo, "si llueve, entonces el suelo estará mojado".

En este ejemplo, la proposición A es "llueve", mientras que la proposición B es "el suelo estará mojado". La implicación establece que si A es verdadero, entonces B también lo será.

¿Qué es el triángulo en la proposición?

El triángulo en la proposición es un símbolo que se utiliza para representar una implicación o condicional. El triángulo se coloca entre las dos proposiciones y se lee como "si A, entonces B".

El triángulo en la proposición se utiliza para representar una implicación de manera más clara y concisa. En lugar de escribir "si A, entonces B", podemos simplemente escribir A seguido del triángulo y luego B.

¿Cómo se utiliza el triángulo en la proposición en la lógica?

El triángulo en la proposición se utiliza en la lógica para construir argumentos y razonamientos. Los argumentos constan de una o más proposiciones y se usan para llegar a una conclusión.

Por ejemplo, podemos construir el siguiente argumento utilizando el triángulo en la proposición:

A: Si llueve, entonces el suelo estará mojado.
B: Está lloviendo.
C: Por lo tanto, el suelo estará mojado.

En este argumento, A es la implicación, B es la proposición que afirma que está lloviendo y C es la conclusión que se deriva de la implicación y la proposición B.

¿Cómo se relaciona el triángulo en la proposición con otros símbolos de la lógica?

El triángulo en la proposición se relaciona con otros símbolos de la lógica, como la negación, la conjunción y la disyunción.

La negación se representa con una línea horizontal encima de una proposición. Por ejemplo, la negación de "llueve" sería "no llueve". La conjunción se representa con un punto entre dos proposiciones. Por ejemplo, "llueve y el suelo está mojado". La disyunción se representa con una V entre dos proposiciones. Por ejemplo, "llueve o no llueve".

El triángulo en la proposición se utiliza en conjunto con estos símbolos para construir argumentos y razonamientos.

Conclusión

El triángulo en la proposición es un símbolo utilizado en la lógica para representar una implicación o condicional entre dos proposiciones. Se utiliza para construir argumentos y razonamientos y es una herramienta útil para simplificar la escritura de implicaciones.

Preguntas frecuentes

¿Qué es una proposición?

Una proposición es una afirmación que puede ser verdadera o falsa.

¿Qué es una implicación o condicional?

Una implicación o condicional es una proposición que establece una relación entre dos proposiciones.

¿Cómo se utiliza el triángulo en la proposición en la lógica?

El triángulo en la proposición se utiliza en la lógica para construir argumentos y razonamientos.

¿Cómo se relaciona el triángulo en la proposición con otros símbolos de la lógica?

El triángulo en la proposición se relaciona con otros símbolos de la lógica, como la negación, la conjunción y la disyunción.

¿Cuál es la importancia del triángulo en la proposición en la lógica?

El triángulo en la proposición es importante en la lógica porque simplifica la escritura de implicaciones y ayuda a construir argumentos y razonamientos de manera más clara y concisa.