Descubre la lógica booleana: significado y aplicaciones
La lógica booleana es un sistema de lógica matemática que utiliza valores booleanos, es decir, valores binarios (1 o 0) para representar afirmaciones verdaderas o falsas. Fue desarrollada por George Boole en el siglo XIX y es ampliamente utilizada en la informática y la electrónica.
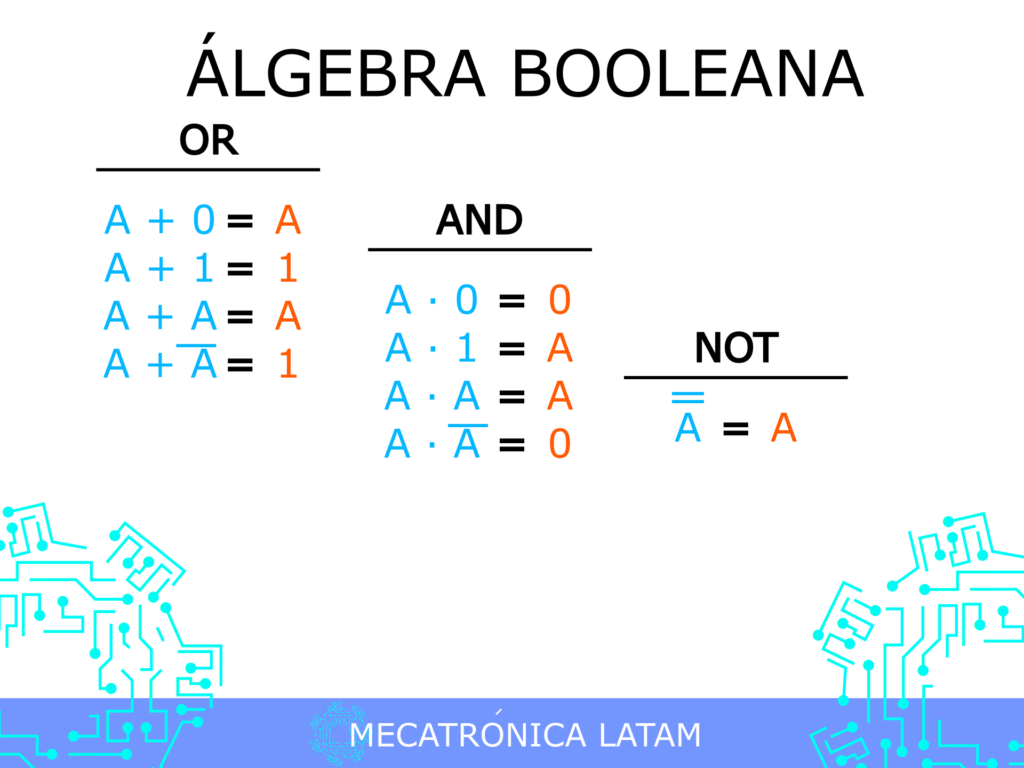
La lógica booleana se basa en tres operadores lógicos principales: AND, OR y NOT. Estos operadores permiten combinar afirmaciones para producir nuevas afirmaciones. Por ejemplo, si tenemos dos afirmaciones A y B, el operador AND (representado por el símbolo & o &&) devuelve verdadero (1) solo si ambas afirmaciones son verdaderas. El operador OR (representado por el símbolo | o ||) devuelve verdadero (1) si al menos una de las afirmaciones es verdadera. Finalmente, el operador NOT (representado por el símbolo !) invierte el valor de la afirmación, es decir, si la afirmación es verdadera, NOT la convierte en falsa y viceversa.
La lógica booleana es ampliamente utilizada en la programación y la electrónica para tomar decisiones basadas en valores binarios. Por ejemplo, en un programa de ordenador, se pueden utilizar afirmaciones booleanas para controlar el flujo de ejecución del programa. Si una afirmación es verdadera, el programa ejecutará una sección de código; si es falsa, el programa ejecutará una sección diferente.
Otra aplicación de la lógica booleana es en los circuitos electrónicos. Los circuitos digitales utilizan transistores para representar afirmaciones booleanas y realizar operaciones lógicas. Los circuitos integrados se construyen utilizando transistores y otros componentes para realizar operaciones complejas utilizando lógica booleana.
La lógica booleana también se utiliza en el diseño de bases de datos y en la búsqueda de información en motores de búsqueda. Los motores de búsqueda utilizan algoritmos que utilizan afirmaciones booleanas para encontrar resultados relevantes. Por ejemplo, si buscas "coches y motos" en un motor de búsqueda, el motor buscará resultados que contengan ambas palabras.
La lógica booleana es una herramienta importante en la programación, la electrónica y la búsqueda de información. Los operadores lógicos AND, OR y NOT permiten combinar afirmaciones para producir nuevas afirmaciones, lo que permite tomar decisiones basadas en valores binarios. La lógica booleana es una herramienta esencial para el diseño de circuitos digitales, bases de datos y motores de búsqueda.
Aplicaciones de la lógica booleana
La lógica booleana se utiliza en una amplia variedad de aplicaciones, incluyendo:
- Control de flujo en programas informáticos.
- Diseño de circuitos electrónicos.
- Búsqueda de información en motores de búsqueda.
- Diseño de bases de datos.
- Análisis y diseño de sistemas de control.
Operadores lógicos principales
Existen tres operadores lógicos principales en la lógica booleana:
- AND: devuelve verdadero solo si ambas afirmaciones son verdaderas.
- OR: devuelve verdadero si al menos una de las afirmaciones es verdadera.
- NOT: invierte el valor de la afirmación.
Ejemplos de uso de la lógica booleana
Aquí hay algunos ejemplos de cómo se puede utilizar la lógica booleana:
- Si una persona es mayor de edad y tiene un carnet de conducir, entonces puede conducir un coche.
- Si una persona tiene un grado universitario o experiencia laboral equivalente, entonces puede solicitar un trabajo.
- Si una persona no tiene antecedentes penales, entonces puede ser contratado como policía.
Tablas de verdad
Las tablas de verdad son una herramienta útil para comprender la lógica booleana. Una tabla de verdad muestra todas las combinaciones posibles de valores de entrada y el resultado correspondiente de la operación lógica. Por ejemplo, aquí hay una tabla de verdad para el operador AND:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
La tabla muestra que la operación AND devuelve verdadero solo si ambas entradas son verdaderas.
Conclusión
La lógica booleana es una herramienta esencial para la programación, la electrónica y la búsqueda de información. Los operadores lógicos AND, OR y NOT permiten combinar afirmaciones para producir nuevas afirmaciones, lo que permite tomar decisiones basadas en valores binarios. La lógica booleana es una herramienta esencial para el diseño de circuitos digitales, bases de datos y motores de búsqueda.
Preguntas frecuentes
¿Por qué se llama lógica booleana?
La lógica booleana se llama así en honor a George Boole, el matemático inglés que la desarrolló en el siglo XIX.
¿Cuál es la aplicación más común de la lógica booleana?
La aplicación más común de la lógica booleana es en la programación de ordenadores y el diseño de circuitos electrónicos.
¿Qué es una tabla de verdad?
Una tabla de verdad es una herramienta útil para comprender la lógica booleana. Muestra todas las combinaciones posibles de valores de entrada y el resultado correspondiente de la operación lógica.
¿Cómo se utiliza la lógica booleana en los motores de búsqueda?
Los motores de búsqueda utilizan algoritmos que utilizan afirmaciones booleanas para encontrar resultados relevantes. Cuando realizas una búsqueda, el motor de búsqueda busca resultados que contengan las palabras clave especificadas utilizando operadores lógicos como AND, OR y NOT.
¿Por qué es importante la lógica booleana?
La lógica booleana es importante porque permite tomar decisiones basadas en valores binarios. Es una herramienta esencial para la programación, la electrónica y la búsqueda de información.
Deja una respuesta