Descubre la importancia del teorema de Lagrange en las matemáticas

Si eres un apasionado de las matemáticas, seguro que conoces el teorema de Lagrange. Este teorema, también conocido como el teorema del valor medio, es uno de los más importantes en el cálculo diferencial. Fue desarrollado por el matemático francés Joseph Louis Lagrange en el siglo XVIII y ha sido utilizado en una gran cantidad de aplicaciones en diversos campos de la ciencia y la ingeniería. En este artículo, descubrirás la importancia del teorema de Lagrange en las matemáticas y cómo se aplica en diferentes contextos.

¿Qué es el teorema de Lagrange?

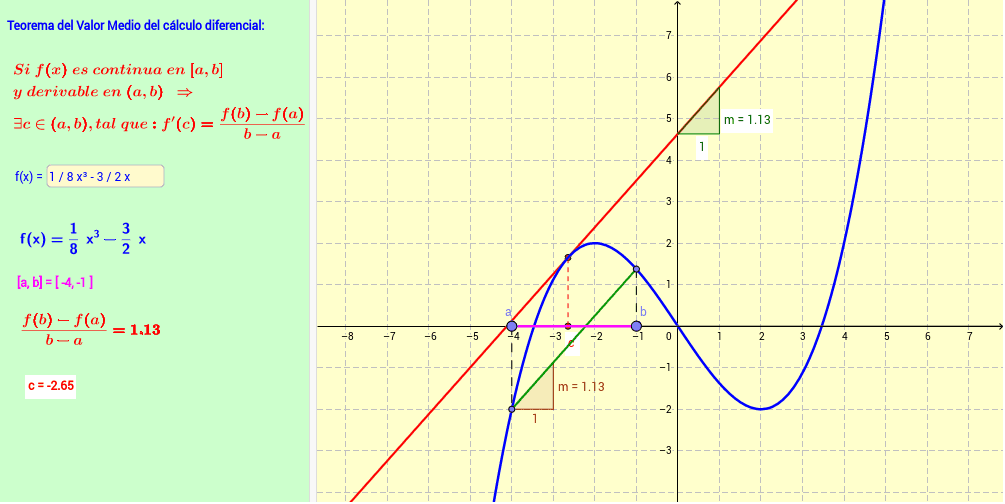
El teorema de Lagrange establece que si una función f(x) es continua en un intervalo cerrado [a,b] y diferenciable en el intervalo abierto (a,b), entonces existe un punto c en el intervalo abierto tal que:

f(b) - f(a) = f'(c)(b-a)

En otras palabras, el teorema de Lagrange nos dice que existe un punto en el intervalo [a,b] donde la pendiente de la función es igual a la pendiente de la recta secante que une los puntos (a,f(a)) y (b,f(b)). Este punto se conoce como el punto medio o el punto de Lagrange.

¿Por qué es importante el teorema de Lagrange?

El teorema de Lagrange es importante en las matemáticas porque permite demostrar una gran cantidad de resultados en cálculo diferencial. Por ejemplo, se puede utilizar para demostrar el teorema de Rolle, que establece que si una función es continua en un intervalo cerrado y diferenciable en el intervalo abierto, y f(a) = f(b), entonces existe un punto c en el intervalo abierto donde la derivada de la función es igual a cero. El teorema de Rolle es importante en la resolución de problemas de optimización y en la determinación de extremos locales de funciones.

Además, el teorema de Lagrange es utilizado en la resolución de problemas de física, como la determinación de la velocidad media de un objeto en movimiento. También se utiliza en la economía, para determinar el valor medio de una función de producción o el valor medio de una función de costos.

¿Cómo se aplica el teorema de Lagrange?

El teorema de Lagrange se aplica en una gran cantidad de problemas matemáticos. Por ejemplo, se puede utilizar para determinar la existencia de puntos críticos de una función, es decir, puntos donde la derivada de la función es cero o no existe. También se puede utilizar para demostrar la existencia de soluciones de ecuaciones diferenciales.

En la física, el teorema de Lagrange se utiliza en la mecánica clásica para determinar las ecuaciones de movimiento de un sistema. Por ejemplo, se puede utilizar para determinar la trayectoria de un proyectil en movimiento, la velocidad de un objeto en caída libre, o la aceleración de un cuerpo en movimiento circular.

En la economía, el teorema de Lagrange se utiliza para determinar la producción óptima de una empresa o el nivel de precios que maximiza los beneficios. También se utiliza para determinar la asignación óptima de recursos en una economía.

¿Cuáles son las limitaciones del teorema de Lagrange?

Aunque el teorema de Lagrange es muy útil en la resolución de problemas matemáticos, también tiene algunas limitaciones. Por ejemplo, solo se puede aplicar a funciones que son continuas y diferenciables en un intervalo cerrado. Además, no siempre es posible encontrar el punto de Lagrange mediante métodos analíticos, lo que puede requerir el uso de métodos numéricos.

Conclusión

El teorema de Lagrange es uno de los más importantes en el cálculo diferencial. Se utiliza en una gran cantidad de aplicaciones en campos tan diversos como la física, la ingeniería y la economía. Su importancia radica en que permite demostrar una gran cantidad de resultados en cálculo diferencial y en la resolución de problemas de optimización. Sin duda, el teorema de Lagrange seguirá siendo una herramienta fundamental en las matemáticas durante muchos años.

Preguntas frecuentes

¿Qué es el teorema de Lagrange?

El teorema de Lagrange establece que si una función f(x) es continua en un intervalo cerrado [a,b] y diferenciable en el intervalo abierto (a,b), entonces existe un punto c en el intervalo abierto tal que: f(b) - f(a) = f'(c)(b-a).

¿Por qué es importante el teorema de Lagrange?

El teorema de Lagrange es importante en las matemáticas porque permite demostrar una gran cantidad de resultados en cálculo diferencial y se utiliza en la resolución de problemas de física, ingeniería y economía.

¿Cómo se aplica el teorema de Lagrange?

El teorema de Lagrange se aplica en una gran cantidad de problemas matemáticos, como la determinación de la existencia de puntos críticos de una función, la resolución de ecuaciones diferenciales, la determinación de las ecuaciones de movimiento de un sistema en física, y la determinación de la producción óptima de una empresa en economía.

¿Cuáles son las limitaciones del teorema de Lagrange?

Las limitaciones del teorema de Lagrange son que solo se puede aplicar a funciones que son continuas y diferenciables en un intervalo cerrado, y no siempre es posible encontrar el punto de Lagrange mediante métodos analíticos.

¿En qué campos se utiliza el teorema de Lagrange?

El teorema de Lagrange se utiliza en campos tan diversos como la física, la ingeniería y la economía.