Descubre la importancia de la teoría de conjuntos en la ciencia

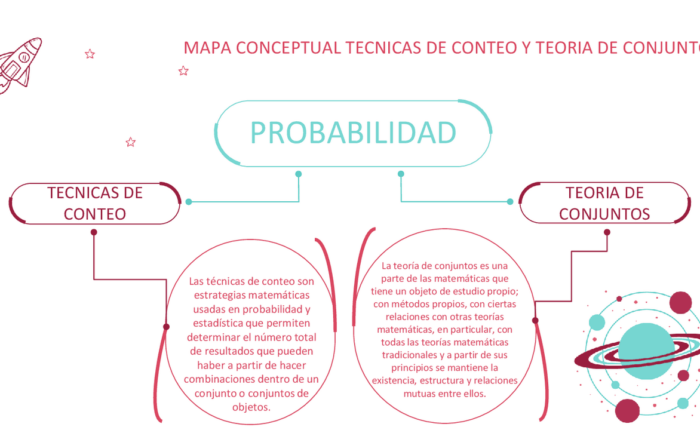
La teoría de conjuntos es una rama fundamental de las matemáticas que tiene una gran importancia en el desarrollo de la ciencia. Esta teoría se encarga de estudiar las relaciones entre conjuntos y cómo estos se relacionan entre sí. En este artículo, exploraremos la relevancia de la teoría de conjuntos en la ciencia, y cómo ha sido utilizada para resolver problemas en diversas disciplinas.

¿Qué es la teoría de conjuntos?

La teoría de conjuntos fue desarrollada por el matemático alemán Georg Cantor a finales del siglo XIX. Esta teoría se encarga de estudiar los conjuntos, que son colecciones de objetos. Por ejemplo, el conjunto de los números enteros positivos, el conjunto de los planetas del sistema solar, el conjunto de las letras del alfabeto, entre otros.

La teoría de conjuntos se basa en una serie de axiomas, que son afirmaciones que se consideran verdaderas sin necesidad de demostración. Entre ellos se encuentra el axioma de extensión, que establece que dos conjuntos son iguales si y solo si tienen los mismos elementos. Este axioma es fundamental para la teoría de conjuntos, ya que permite definir de manera precisa qué es un conjunto.

Aplicaciones de la teoría de conjuntos en la ciencia

La teoría de conjuntos es una herramienta fundamental en el desarrollo de la ciencia. A continuación, se presentan algunas de las aplicaciones de la teoría de conjuntos en diferentes disciplinas:

Probabilidad

En la teoría de la probabilidad, los conjuntos juegan un papel fundamental en el cálculo de las probabilidades de ocurrencia de eventos. Por ejemplo, si se tiene un conjunto de posibles resultados de un experimento, se puede calcular la probabilidad de que un evento en particular ocurra como la proporción del número de elementos del conjunto que corresponden al evento sobre el número total de elementos del conjunto.

Topología

La topología es una rama de las matemáticas que se encarga de estudiar las propiedades de los espacios y sus transformaciones. La teoría de conjuntos es esencial en la topología ya que permite definir de manera precisa los conceptos de abierto, cerrado, límite, entre otros.

Lógica

La lógica es la ciencia que se encarga de estudiar el razonamiento humano. La teoría de conjuntos se utiliza en la lógica para definir los conceptos de proposición, conjunto de proposiciones, operaciones lógicas, entre otros.

Informática

En informática, la teoría de conjuntos se utiliza en la teoría de la computación y en la programación. Los conjuntos se utilizan para representar datos, como por ejemplo los conjuntos de números primos, los conjuntos de palabras en un diccionario, entre otros.

Conclusiones

La teoría de conjuntos es una rama fundamental de las matemáticas que tiene una gran importancia en el desarrollo de la ciencia. Esta teoría se utiliza en diversas disciplinas, como la probabilidad, la topología, la lógica y la informática, entre otras. Los conjuntos permiten definir de manera precisa los conceptos y relaciones entre objetos, lo que la convierte en una herramienta indispensable para el avance de la ciencia.

Preguntas frecuentes

¿Qué es un conjunto?

Un conjunto es una colección de objetos que se consideran como una sola entidad.

¿Cuál es el axioma fundamental de la teoría de conjuntos?

El axioma de extensión es el axioma fundamental de la teoría de conjuntos, ya que establece que dos conjuntos son iguales si y solo si tienen los mismos elementos.

¿En qué disciplinas se utiliza la teoría de conjuntos?

La teoría de conjuntos se utiliza en diversas disciplinas, como la probabilidad, la topología, la lógica y la informática, entre otras.

¿Cómo se utilizan los conjuntos en la probabilidad?

En la teoría de la probabilidad, los conjuntos se utilizan para representar los posibles resultados de un experimento, lo que permite calcular las probabilidades de ocurrencia de eventos.

¿Qué es la topología?

La topología es una rama de las matemáticas que se encarga de estudiar las propiedades de los espacios y sus transformaciones.