Descubre la hipótesis de Riemann de forma sencilla y clara
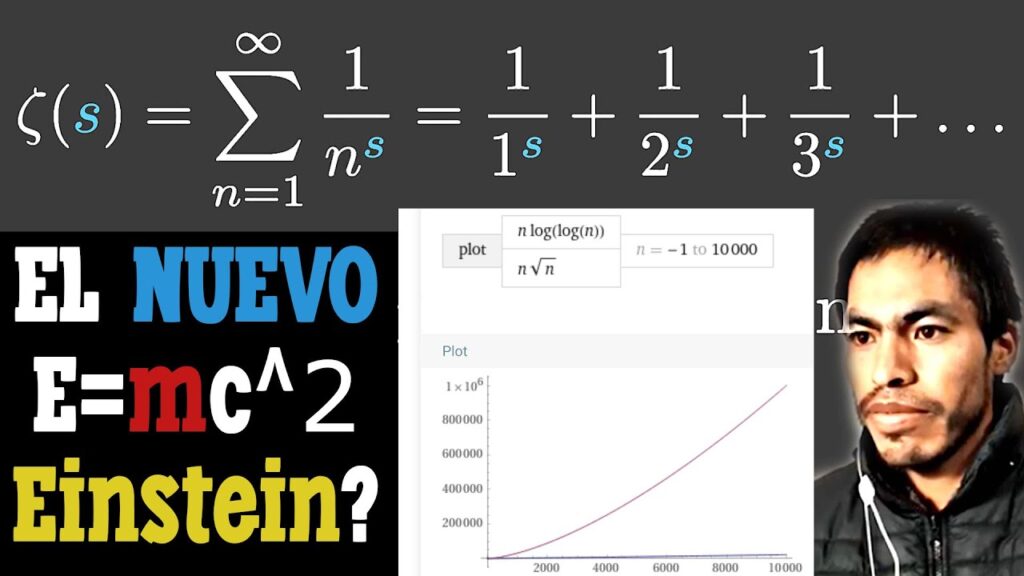
La hipótesis de Riemann es uno de los problemas más grandes y enigmáticos de las matemáticas modernas. Fue formulada por el matemático alemán Bernhard Riemann en 1859 y hasta el día de hoy, sigue siendo uno de los problemas sin resolver más importantes en la teoría de números. En este artículo, te explicaremos en términos sencillos y claros qué es la hipótesis de Riemann, su importancia y cómo se relaciona con la distribución de números primos.
- ¿Qué es la hipótesis de Riemann?
- ¿Por qué es importante la hipótesis de Riemann?
- ¿Cómo se relaciona la hipótesis de Riemann con los números primos?
- ¿Cómo se han tratado de resolver la hipótesis de Riemann?
- ¿Por qué la hipótesis de Riemann sigue siendo un problema sin resolver?
- Conclusión
- Preguntas frecuentes
¿Qué es la hipótesis de Riemann?
La hipótesis de Riemann es una conjetura sobre la distribución de los números primos. En esencia, dice que la frecuencia de los números primos está relacionada con la distribución de los ceros de la función zeta de Riemann. Esta función matemática, denotada como ζ(s), está definida para todos los números complejos s con una parte real mayor que 1. Su fórmula es:
ζ(s) = 1 + 1/2^s + 1/3^s + 1/4^s + ...
La hipótesis de Riemann sugiere que todos los ceros no triviales de la función zeta de Riemann (es decir, los que no son 1, 2, 3, ...) tienen una parte real de 1/2. Es decir, si s = 1/2 + ti es un cero no trivial de ζ(s), entonces la hipótesis de Riemann dice que t = 0. Esta hipótesis es importante porque está relacionada con la distribución de los números primos.
¿Por qué es importante la hipótesis de Riemann?
La hipótesis de Riemann es importante porque está relacionada con la distribución de los números primos. Los números primos son los números enteros que solo son divisibles por 1 y por sí mismos. Estos números son de gran importancia en la teoría de números y tienen muchas aplicaciones prácticas, como en la criptografía.
La distribución de los números primos es muy irregular e impredecible. Por ejemplo, hay muchos más números primos pequeños que grandes. La hipótesis de Riemann sugiere que la distribución de los números primos está estrechamente relacionada con la ubicación de los ceros no triviales de la función zeta de Riemann. Si la hipótesis de Riemann es cierta, entonces se podría obtener información muy valiosa sobre la distribución de los números primos.
¿Cómo se relaciona la hipótesis de Riemann con los números primos?
La relación entre la hipótesis de Riemann y los números primos se basa en la función zeta de Riemann. Esta función tiene la propiedad de que, para s con parte real mayor que 1, ζ(s) puede expresarse como el producto de la serie infinita de fracciones:
ζ(s) = 1/(1-p^-s) * 1/(1-2^-s) * 1/(1-3^-s) * ...
Donde p son los números primos. Esta relación significa que la función zeta de Riemann está estrechamente relacionada con la distribución de los números primos. La hipótesis de Riemann sugiere que la ubicación de los ceros no triviales de la función zeta de Riemann está relacionada con la distribución de los números primos.
¿Cómo se han tratado de resolver la hipótesis de Riemann?
A lo largo de los años, muchos matemáticos han tratado de resolver la hipótesis de Riemann. Hasta el momento, nadie ha sido capaz de demostrar si es cierta o falsa. Sin embargo, hay algunas aproximaciones que pueden dar pistas sobre la veracidad de la hipótesis.
Una de las aproximaciones más importantes es la teoría de los números algebraicos. Esta teoría establece una conexión entre la hipótesis de Riemann y la teoría de Galois. También se han desarrollado métodos computacionales para buscar ceros no triviales de la función zeta de Riemann. Esta búsqueda ha encontrado muchos ceros en la línea crítica, pero no ha sido capaz de demostrar la hipótesis de Riemann.
¿Por qué la hipótesis de Riemann sigue siendo un problema sin resolver?
La hipótesis de Riemann sigue siendo un problema sin resolver porque nadie ha sido capaz de demostrar si es verdadera o falsa. A pesar de que se han hecho muchos avances en la teoría de números, la hipótesis de Riemann sigue siendo uno de los mayores enigmas de las matemáticas modernas. La complejidad de la función zeta de Riemann y la irregularidad de la distribución de los números primos hacen que sea muy difícil demostrar la hipótesis.
Conclusión
La hipótesis de Riemann es uno de los mayores enigmas de las matemáticas modernas. Fue formulada por el matemático alemán Bernhard Riemann en 1859 y hasta el día de hoy, sigue siendo uno de los problemas sin resolver más importantes en la teoría de números. La hipótesis de Riemann sugiere que la distribución de los números primos está estrechamente relacionada con la ubicación de los ceros no triviales de la función zeta de Riemann. Si la hipótesis de Riemann es cierta, entonces se podría obtener información muy valiosa sobre la distribución de los números primos. A pesar de que se han hecho muchos avances en la teoría de números, la hipótesis de Riemann sigue siendo uno de los mayores enigmas de las matemáticas modernas.
Preguntas frecuentes
¿Qué es la función zeta de Riemann?
La función zeta de Riemann es una función matemática que está definida para todos los números complejos s con una parte real mayor que 1. Su fórmula es ζ(s) = 1 + 1/2^s + 1/3^s + 1/4^s + ...
¿Qué son los números primos?
Los números primos son los números enteros que solo son divisibles por 1 y por sí mismos. Estos números son de gran importancia en la teoría de números y tienen muchas aplicaciones prácticas, como en la criptografía.
¿Por qué la hipótesis de Riemann es importante?
La hipótesis de Riemann es importante porque está relacionada con la distribución de los números primos. Si es cierta, se podría obtener información muy valiosa sobre la distribución de los números primos.
¿Qué es la línea crítica?
La línea crítica es una línea imaginaria en el plano complejo donde se encuentran los ceros no triviales de la función zeta de Riemann. Según la hipótesis de Riemann, todos los ceros no triviales de la función zeta de Riemann están en la línea crítica.
¿Cómo se ha tratado de resolver la hipótesis de Riemann?
Se han
Deja una respuesta