Descubre la fórmula de la hipótesis de Riemann en este artículo

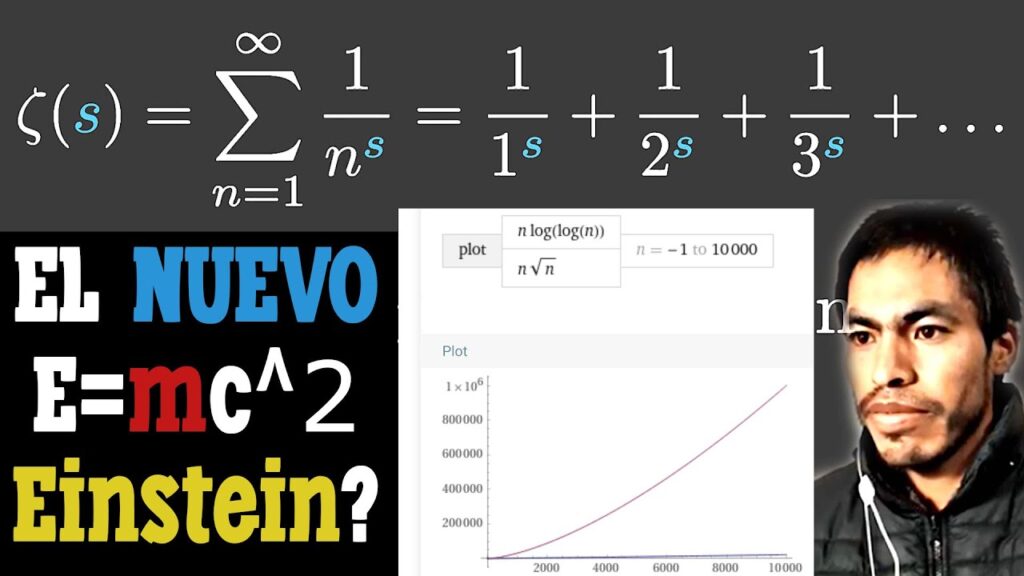
La hipótesis de Riemann es uno de los mayores misterios sin resolver en las matemáticas. Esta hipótesis establece que todos los ceros no triviales de la función zeta de Riemann tienen una parte real de 1/2. En otras palabras, si graficamos los ceros de la función zeta de Riemann en un plano complejo, todos ellos estarán en una línea vertical que corre a través de 1/2 en el eje x. Esta hipótesis es fundamental para entender la distribución de los números primos, y su resolución es uno de los problemas más importantes en las matemáticas contemporáneas.

En este artículo, descubriremos la fórmula de la hipótesis de Riemann y exploraremos su importancia en las matemáticas.

¿Qué es la función zeta de Riemann?

Para entender la hipótesis de Riemann, primero debemos entender la función zeta de Riemann. Esta función es una función matemática que se define para todos los números complejos s con una parte real mayor que 1. Se define como:

zeta(s) = 1 + 1/2^s + 1/3^s + 1/4^s + ...

Esta función es importante porque está relacionada con la distribución de los números primos. De hecho, la hipótesis de Riemann establece que la distribución de los números primos está estrechamente relacionada con los ceros de la función zeta de Riemann.

¿Qué son los ceros de la función zeta de Riemann?

Los ceros de la función zeta de Riemann son los valores de s para los cuales la función zeta(s) es igual a cero. Estos valores son importantes porque están relacionados con la distribución de los números primos.

La hipótesis de Riemann establece que todos los ceros no triviales de la función zeta de Riemann tienen una parte real de 1/2. Esto significa que si graficamos los ceros de la función zeta de Riemann en un plano complejo, todos ellos estarán en una línea vertical que corre a través de 1/2 en el eje x.

La fórmula de la hipótesis de Riemann

La fórmula de la hipótesis de Riemann es una expresión matemática que relaciona los ceros de la función zeta de Riemann con los números primos. Esta fórmula se conoce como la función explícita de la función zeta de Riemann y se define como:

ζ(s) = 2^s π^(s-1) sin(πs/2) Γ(1-s) ζ(1-s)

donde Γ(s) es la función gamma compleja.

Esta fórmula es importante porque permite a los matemáticos calcular los valores de la función zeta de Riemann para cualquier valor de s, incluyendo los ceros no triviales de la función zeta de Riemann.

La importancia de la hipótesis de Riemann

La hipótesis de Riemann es importante porque está estrechamente relacionada con la distribución de los números primos. En particular, la hipótesis de Riemann establece que la distribución de los números primos está estrechamente relacionada con los ceros de la función zeta de Riemann.

Si la hipótesis de Riemann es verdadera, entonces se pueden hacer predicciones precisas sobre la distribución de los números primos. Por ejemplo, se puede predecir el número de números primos menores que un número dado. Además, la resolución de la hipótesis de Riemann tendría importantes implicaciones en la criptografía y en la teoría de números en general.

Conclusión

La hipótesis de Riemann es uno de los mayores misterios sin resolver en las matemáticas. Esta hipótesis establece que todos los ceros no triviales de la función zeta de Riemann tienen una parte real de 1/2. La fórmula de la hipótesis de Riemann relaciona los ceros de la función zeta de Riemann con los números primos y es importante porque permite a los matemáticos calcular los valores de la función zeta de Riemann para cualquier valor de s, incluyendo los ceros no triviales de la función zeta de Riemann. La resolución de la hipótesis de Riemann tendría importantes implicaciones en la criptografía y en la teoría de números en general.

Preguntas frecuentes

¿Qué es la hipótesis de Riemann?

La hipótesis de Riemann establece que todos los ceros no triviales de la función zeta de Riemann tienen una parte real de 1/2.

¿Qué son los ceros de la función zeta de Riemann?

Los ceros de la función zeta de Riemann son los valores de s para los cuales la función zeta(s) es igual a cero.

¿Por qué es importante la hipótesis de Riemann?

La hipótesis de Riemann es importante porque está estrechamente relacionada con la distribución de los números primos. Además, la resolución de la hipótesis de Riemann tendría importantes implicaciones en la criptografía y en la teoría de números en general.

¿Qué es la función zeta de Riemann?

La función zeta de Riemann es una función matemática que se define para todos los números complejos s con una parte real mayor que 1. Se define como: zeta(s) = 1 + 1/2^s + 1/3^s + 1/4^s + ...

¿Cómo se relaciona la hipótesis de Riemann con los números primos?

La hipótesis de Riemann establece que la distribución de los números primos está estrechamente relacionada con los ceros de la función zeta de Riemann. En particular, si la hipótesis de Riemann es verdadera, entonces se pueden hacer predicciones precisas sobre la distribución de los números primos.