Descubre la disyunción inclusiva: ejemplos claros y sencillos

¿Alguna vez has escuchado el término "disyunción inclusiva"? Este concepto es muy común en el ámbito lógico y matemático, pero puede resultar confuso para aquellos que no están familiarizados con él. En este artículo, te explicaremos qué es la disyunción inclusiva y te daremos algunos ejemplos claros y sencillos para que puedas entenderlo fácilmente.

¿Qué es la disyunción inclusiva?

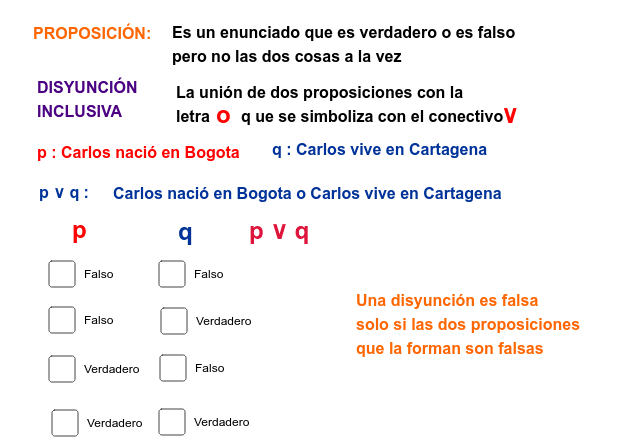
La disyunción inclusiva es un término utilizado en lógica y matemáticas que se refiere a una operación lógica que se utiliza para unir dos o más proposiciones. Esta operación se representa con el símbolo "o", pero a diferencia de la disyunción exclusiva, en la disyunción inclusiva se acepta que ambas proposiciones pueden ser verdaderas al mismo tiempo.

En otras palabras, la disyunción inclusiva es una forma de unir dos o más afirmaciones para crear una nueva afirmación que es verdadera si al menos una de las afirmaciones originales es verdadera.

Ejemplos de disyunción inclusiva

Para entender mejor la disyunción inclusiva, veamos algunos ejemplos:

- "Me gusta el chocolate o me gusta el helado": En este ejemplo, hay dos afirmaciones que se unen mediante la disyunción inclusiva. Si a alguien le gusta el chocolate o el helado, entonces la afirmación completa es verdadera.

- "El examen será el lunes o el martes": En este caso, la afirmación es verdadera si el examen se lleva a cabo en cualquiera de los dos días mencionados.

- "El cielo está nublado o está lloviendo": Si el cielo está nublado o está lloviendo, entonces la afirmación completa es verdadera.

Diferencia entre disyunción inclusiva y exclusiva

Es importante destacar que la disyunción inclusiva es diferente a la disyunción exclusiva. En la disyunción exclusiva, sólo una de las dos proposiciones puede ser verdadera, mientras que en la disyunción inclusiva ambas proposiciones pueden ser verdaderas simultáneamente.

Por ejemplo, "Me gusta el chocolate o me gusta el helado" es un ejemplo de disyunción inclusiva, mientras que "Me gusta el chocolate o el helado, pero no ambos" es un ejemplo de disyunción exclusiva.

Usos de la disyunción inclusiva

La disyunción inclusiva se utiliza comúnmente en matemáticas y lógica, pero también se puede aplicar en situaciones cotidianas. Por ejemplo, en una tienda de ropa, una etiqueta podría decir "la camisa es de algodón o de poliéster" para indicar los materiales disponibles.

En la programación, la disyunción inclusiva se utiliza para crear condiciones en las que se pueden cumplir varias alternativas. Por ejemplo, un programa podría preguntar: "¿Quieres una pizza o una hamburguesa?" y si el usuario responde "pizza", el programa ejecutará el código correspondiente a la opción de pizza.

Conclusión

La disyunción inclusiva es una operación lógica que se utiliza para unir dos o más afirmaciones y crear una nueva afirmación que es verdadera si al menos una de las afirmaciones originales es verdadera. Es importante diferenciarla de la disyunción exclusiva, que sólo permite que una de las dos proposiciones sea verdadera. La disyunción inclusiva se utiliza comúnmente en matemáticas, lógica y programación, pero también puede aplicarse en situaciones cotidianas.

Preguntas frecuentes

1. ¿Por qué se llama "inclusiva"?

Se llama "inclusiva" porque acepta que ambas proposiciones pueden ser verdaderas al mismo tiempo.

2. ¿La disyunción inclusiva sólo se aplica a dos proposiciones?

No, la disyunción inclusiva puede aplicarse a dos o más proposiciones.

3. ¿Cómo se representa la disyunción inclusiva?

La disyunción inclusiva se representa con el símbolo "o".

4. ¿La disyunción inclusiva se utiliza únicamente en matemáticas y lógica?

No, la disyunción inclusiva también se puede aplicar en situaciones cotidianas y en programación.

5. ¿La disyunción exclusiva es lo mismo que la negación?

No, la negación es una operación lógica que se utiliza para negar una afirmación, mientras que la disyunción exclusiva es una operación lógica que se utiliza para unir dos proposiciones con la condición de que sólo una de ellas sea verdadera.