Descubre la diferencia entre V y V invertida en lógica

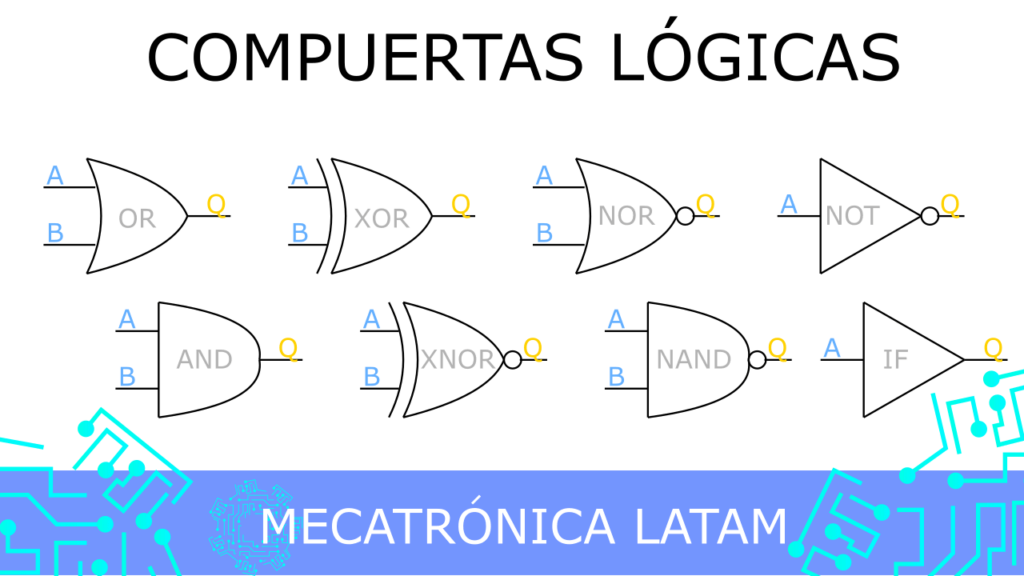
Cuando se trata de la lógica, es importante entender los diferentes símbolos y operadores que se utilizan para representar proposiciones y relaciones entre ellas. En particular, es común encontrarse con dos símbolos que a simple vista parecen iguales, pero que en realidad tienen significados muy distintos: V y V invertida. En este artículo, te explicaremos la diferencia entre ambos y cómo se usan en la lógica.

¿Qué es la lógica?

Antes de entrar en detalle sobre los símbolos V y V invertida, es importante entender qué es la lógica. En términos generales, la lógica es la disciplina que se encarga de estudiar los principios y métodos que rigen el pensamiento humano, con el objetivo de establecer criterios objetivos para la verdad y la validez de los argumentos.

En la lógica, se utilizan símbolos y operadores para representar proposiciones y relaciones entre ellas. Estos símbolos y operadores tienen un significado preciso y se utilizan para construir argumentos y demostraciones.

V y V invertida: ¿qué son?

V y V invertida son dos símbolos que se utilizan en la lógica para representar operaciones lógicas. A primera vista, ambos símbolos parecen iguales, ya que tienen una forma similar y se escriben de la misma manera. Sin embargo, su significado es muy diferente.

El símbolo V representa la operación lógica de disyunción, que se utiliza para unir dos proposiciones. Por ejemplo, si tenemos las proposiciones "Ana es alta" y "Juan es bajo", podemos unirlas mediante la disyunción, de la siguiente manera: "Ana es alta V Juan es bajo". Esta proposición es verdadera si al menos una de las dos proposiciones es verdadera.

Por otro lado, el símbolo V invertida representa la operación lógica de conjunción, que se utiliza para relacionar dos proposiciones. Por ejemplo, si tenemos las proposiciones "Ana es alta" y "Juan es bajo", podemos relacionarlas mediante la conjunción, de la siguiente manera: "Ana es alta ^ Juan es bajo". Esta proposición es verdadera sólo si ambas proposiciones son verdaderas.

Ejemplos de uso de V y V invertida

Para entender mejor la diferencia entre V y V invertida, vamos a ver algunos ejemplos de cómo se utilizan en la lógica.

Supongamos que queremos representar la siguiente proposición: "Si llueve, me quedo en casa. Si hace sol, voy a la playa". Podemos unir estas dos proposiciones mediante la disyunción, de la siguiente manera: "Si llueve V si hace sol". Esta proposición es verdadera si se cumple al menos una de las dos proposiciones.

Ahora, supongamos que queremos representar la proposición "Si llueve y hace frío, me quedo en casa". En este caso, debemos utilizar la conjunción, de la siguiente manera: "Si llueve ^ hace frío". Esta proposición es verdadera sólo si ambas proposiciones son verdaderas.

Usos avanzados de V y V invertida

Además de los usos básicos de V y V invertida que hemos visto hasta ahora, existen otras aplicaciones más avanzadas de estos símbolos en la lógica.

Por ejemplo, en la teoría de conjuntos, se utilizan los símbolos V y V invertida para representar la unión y la intersección de conjuntos, respectivamente. En este caso, la disyunción representa la unión de dos conjuntos, mientras que la conjunción representa la intersección de dos conjuntos.

También es común utilizar estos símbolos en la programación, para representar condiciones lógicas en los programas y algoritmos. En este caso, se utilizan los operadores || y && para representar la disyunción y la conjunción, respectivamente.

Conclusión

V y V invertida son dos símbolos que se utilizan en la lógica para representar operaciones lógicas. El símbolo V representa la disyunción, que se utiliza para unir dos proposiciones, mientras que el símbolo V invertida representa la conjunción, que se utiliza para relacionar dos proposiciones. Es importante entender la diferencia entre ambos símbolos para poder construir argumentos lógicos y demostraciones precisas.

Preguntas frecuentes

1. ¿Por qué es importante entender la diferencia entre V y V invertida?

Es importante entender la diferencia entre V y V invertida para poder construir argumentos lógicos precisos y demostraciones válidas. Si confundimos estos dos símbolos, podemos llegar a conclusiones erróneas y cometer errores en nuestras demostraciones.

2. ¿Cómo se utilizan V y V invertida en la teoría de conjuntos?

En la teoría de conjuntos, V y V invertida se utilizan para representar la unión y la intersección de conjuntos, respectivamente. La disyunción representa la unión de dos conjuntos, mientras que la conjunción representa la intersección de dos conjuntos.

3. ¿Se pueden utilizar otros símbolos para representar la disyunción y la conjunción?

Sí, existen otros símbolos que se utilizan para representar la disyunción y la conjunción en la lógica. Por ejemplo, en algunas notaciones lógicas se utilizan los símbolos + y * para representar la disyunción y la conjunción, respectivamente.

4. ¿Cómo se utilizan V y V invertida en la programación?

En la programación, se utilizan los operadores || y && para representar la disyunción y la conjunción, respectivamente. Estos operadores se utilizan para construir condiciones lógicas en los programas y algoritmos.

5. ¿Qué otros operadores lógicos se utilizan en la lógica?

Además de la disyunción y la conjunción, en la lógica se utilizan otros operadores lógicos, como la negación, la implicación y la equivalencia. Estos operadores se utilizan para construir argumentos y demostraciones lógicas más complejas.