Descubre la base de la lógica: Proposiciones simples en matemáticas

La lógica es una rama de las matemáticas que se encarga de estudiar el razonamiento y la argumentación. Es una herramienta fundamental en la solución de problemas y en la toma de decisiones. En este artículo te explicaremos qué son las proposiciones simples en matemáticas, la base de la lógica.

¿Qué son las proposiciones simples?

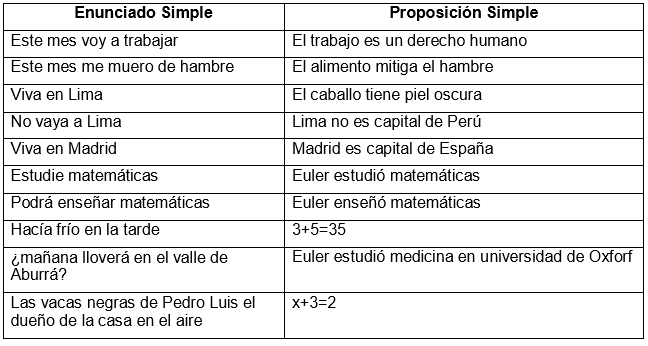
En matemáticas, una proposición es una afirmación que es verdadera o falsa, pero no ambas cosas a la vez. Una proposición simple es aquella que no se puede descomponer en otras proposiciones más pequeñas. Por ejemplo, la afirmación "2+2=4" es una proposición simple, ya que no se puede dividir en proposiciones más pequeñas.

Elementos de una proposición simple

Toda proposición simple está compuesta por dos elementos: el sujeto y el predicado. El sujeto es aquello de lo que se está hablando, y el predicado es lo que se dice del sujeto. Por ejemplo, en la proposición "El cielo es azul", el sujeto es "el cielo" y el predicado es "es azul".

Conectores lógicos

Los conectores lógicos son palabras o símbolos que se utilizan para unir dos o más proposiciones, formando así una proposición compuesta. Los conectores más comunes son "y", "o" y "no". Por ejemplo, la proposición compuesta "El cielo es azul y el sol está brillando" está formada por dos proposiciones simples unidas por el conector lógico "y".

Tablas de verdad

Las tablas de verdad son herramientas que se utilizan para determinar el valor de verdad de una proposición compuesta en función del valor de verdad de sus proposiciones simples. En una tabla de verdad, se representan todas las posibles combinaciones de valores de verdad de las proposiciones simples que forman la proposición compuesta.

Ejemplos de proposiciones simples y compuestas

- Proposición simple: 5 es un número par.
- Proposición simple: El sol es una estrella.
- Proposición compuesta: Si llueve, me quedo en casa.
- Proposición compuesta: El perro ladra y el gato maúlla.

Aplicaciones de las proposiciones simples en matemáticas

Las proposiciones simples son la base de la lógica y se utilizan en muchos campos de las matemáticas, como la geometría, la teoría de conjuntos y la teoría de números. Por ejemplo, en la geometría, las proposiciones simples se utilizan para definir los axiomas y teoremas, y en la teoría de conjuntos, se utilizan para definir las operaciones y relaciones entre conjuntos.

Conclusión

Las proposiciones simples son la base de la lógica y se utilizan en muchas ramas de las matemáticas. Comprender su estructura y cómo se relacionan entre sí es fundamental para el estudio de la lógica y la solución de problemas matemáticos.

Preguntas frecuentes

1. ¿Qué es una proposición en matemáticas?

Una proposición en matemáticas es una afirmación que es verdadera o falsa, pero no ambas cosas a la vez.

2. ¿Qué es una proposición simple?

Una proposición simple es aquella que no se puede descomponer en otras proposiciones más pequeñas.

3. ¿Qué son los conectores lógicos?

Los conectores lógicos son palabras o símbolos que se utilizan para unir dos o más proposiciones, formando así una proposición compuesta.

4. ¿Qué son las tablas de verdad?

Las tablas de verdad son herramientas que se utilizan para determinar el valor de verdad de una proposición compuesta en función del valor de verdad de sus proposiciones simples.

5. ¿Para qué se utilizan las proposiciones simples en las matemáticas?

Las proposiciones simples son la base de la lógica y se utilizan en muchas ramas de las matemáticas, como la geometría, la teoría de conjuntos y la teoría de números.