Descubre la altura h: fórmulas y ejemplos prácticos
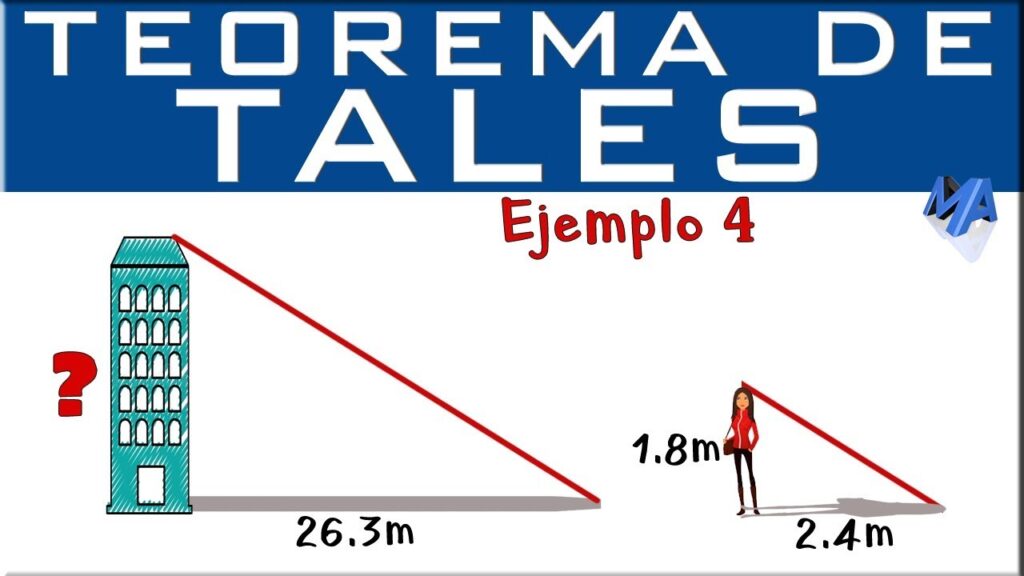
¿Alguna vez has querido saber la altura de un objeto, pero no sabes cómo medirla? La altura h es una medida importante en muchas áreas, desde la arquitectura hasta la física. Afortunadamente, existen fórmulas y ejemplos prácticos que te ayudarán a descubrir la altura h de un objeto.
¿Qué es la altura h?
La altura h es una medida que se refiere a la distancia vertical desde la base de un objeto hasta su punto más alto. Por ejemplo, si estás midiendo la altura de una casa, la altura h se mediría desde la base de la casa hasta el punto más alto del techo. La altura h se utiliza en muchas situaciones, como en la construcción, la arquitectura, la física y la geometría.
Fórmulas para calcular la altura h
Existen varias fórmulas que pueden ayudarte a calcular la altura h de un objeto. Estas son algunas de las fórmulas más comunes:
Fórmula de la trigonometría
Si conoces la longitud de un lado y el ángulo opuesto de un triángulo rectángulo, puedes utilizar la fórmula de la trigonometría para calcular la altura h. La fórmula es la siguiente:
h = b * tan(a)
Donde b es la longitud del lado opuesto al ángulo a, y tan(a) es la tangente del ángulo a.
Fórmula del área de un triángulo
Otra forma de calcular la altura h es utilizando la fórmula del área de un triángulo. La fórmula es la siguiente:
h = (2 * A) / b
Donde A es el área del triángulo y b es la longitud de la base.
Fórmula de la física
En la física, la altura h se puede calcular utilizando la fórmula de la energía potencial gravitatoria. La fórmula es la siguiente:
h = (Epg / m * g)
Donde Epg es la energía potencial gravitatoria, m es la masa del objeto y g es la aceleración debido a la gravedad.
Ejemplos prácticos de cómo calcular la altura h
Ahora que conoces las fórmulas para calcular la altura h, veamos algunos ejemplos prácticos:
Ejemplo 1: Calculando la altura de un edificio
Imagina que quieres calcular la altura de un edificio. Para hacerlo, necesitas medir la longitud de un lado y el ángulo opuesto. Supongamos que la longitud del lado opuesto es de 50 metros y el ángulo opuesto es de 60 grados. Utilizando la fórmula de la trigonometría, podemos calcular la altura h:
h = 50 * tan(60) = 86.6 metros
Por lo tanto, la altura del edificio es de 86.6 metros.
Ejemplo 2: Calculando la altura de un triángulo
Supongamos que quieres calcular la altura de un triángulo con una base de 10 metros y un área de 30 metros cuadrados. Para hacerlo, puedes utilizar la fórmula del área de un triángulo:
h = (2 * 30) / 10 = 6 metros
Por lo tanto, la altura del triángulo es de 6 metros.
Ejemplo 3: Calculando la altura de un objeto utilizando la física
Supongamos que quieres calcular la altura de un objeto de 1000 kg utilizando la fórmula de la física. Si la energía potencial gravitatoria es de 5000 J y la aceleración debido a la gravedad es de 9.8 m/s^2, podemos calcular la altura h:
h = (5000 / (1000 * 9.8)) = 0.51 metros
Por lo tanto, la altura del objeto es de 0.51 metros.
Preguntas frecuentes sobre la altura h
¿Por qué es importante conocer la altura h?
La altura h es una medida importante en muchas áreas, desde la arquitectura hasta la física. Conocer la altura h de un objeto puede ayudarte a realizar cálculos precisos y a tomar decisiones informadas en diferentes situaciones.
¿Qué unidades se utilizan para medir la altura h?
La altura h se puede medir en diferentes unidades, como metros, pies, pulgadas, centímetros, entre otras.
¿Cómo se mide la altura h de un objeto?
La altura h se puede medir utilizando diferentes herramientas, como cintas métricas, reglas, niveles, teodolitos, entre otros.
¿Qué es la altura relativa?
La altura relativa se refiere a la diferencia de altura entre dos objetos o puntos de referencia. Por ejemplo, si quieres calcular la altura relativa entre dos edificios, necesitas conocer la altura de ambos edificios y restarlas.
¿Qué es la altura máxima?
La altura máxima se refiere al punto más alto de un objeto o de un movimiento. Por ejemplo, si estás midiendo la altura máxima de un salto, necesitas medir la altura desde el punto más bajo hasta el punto más alto del salto.
Deja una respuesta