Descubre el teorema de Pitágoras: Ejemplos prácticos

El teorema de Pitágoras es uno de los conceptos más importantes en la geometría, y es utilizado en una gran variedad de situaciones en la vida cotidiana, desde la construcción de edificios hasta la medición de distancias y la resolución de problemas matemáticos.

En este artículo, exploraremos el teorema de Pitágoras en detalle y presentaremos algunos ejemplos prácticos para ilustrar cómo se puede aplicar en situaciones del mundo real.

¿Qué es el teorema de Pitágoras?

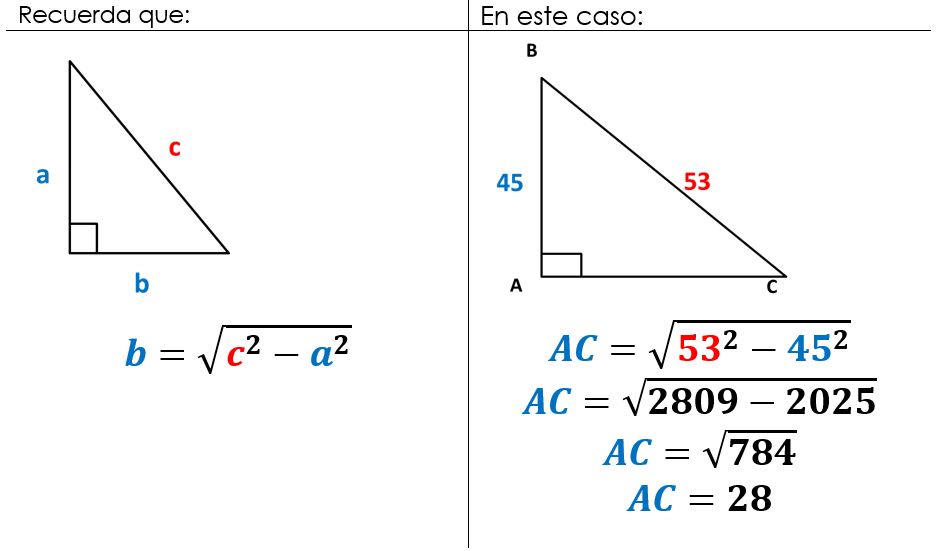
El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados (las catetos).

En términos matemáticos, el teorema puede expresarse de la siguiente manera:

a² + b² = c²

Donde "a" y "b" representan las longitudes de los catetos, y "c" representa la longitud de la hipotenusa.

Ejemplos prácticos de aplicación del teorema de Pitágoras

A continuación, presentamos algunos ejemplos prácticos de situaciones en las que se puede aplicar el teorema de Pitágoras:

1. Construcción de edificios

El teorema de Pitágoras es fundamental en la construcción de edificios y estructuras. Por ejemplo, los arquitectos y los ingenieros utilizan el teorema para calcular las medidas de los marcos de las puertas y ventanas, así como para determinar la altura de las paredes y la longitud de las vigas.

2. Medición de distancias

El teorema de Pitágoras también es útil para medir distancias en terrenos irregulares. Por ejemplo, si se sabe la distancia horizontal entre dos puntos y la diferencia de altitud entre ellos, se puede utilizar el teorema para calcular la distancia real entre los dos puntos.

3. Resolución de problemas matemáticos

El teorema de Pitágoras se utiliza en una gran cantidad de problemas matemáticos, desde la resolución de ecuaciones hasta la estadística y la geometría. Por ejemplo, se puede utilizar para calcular la distancia entre dos puntos en un plano de coordenadas, o para determinar la ubicación de un objeto en el espacio tridimensional.

Cómo aplicar el teorema de Pitágoras

Para aplicar el teorema de Pitágoras, sigue los siguientes pasos:

1. Identifica el triángulo rectángulo y etiqueta los lados (catetos e hipotenusa).
2. Usa la fórmula a² + b² = c² para calcular la longitud del lado desconocido.
3. Resuelve la ecuación para encontrar el valor del lado desconocido.

Conclusión

El teorema de Pitágoras es un concepto fundamental en la geometría y se utiliza en una gran variedad de situaciones en la vida cotidiana. Al comprender cómo aplicar el teorema en situaciones del mundo real, puedes desarrollar una comprensión más profunda de la geometría y mejorar tus habilidades matemáticas en general.

Preguntas frecuentes

1. ¿Qué es un triángulo rectángulo?

Un triángulo rectángulo es un tipo de triángulo en el que uno de los ángulos mide 90 grados (es decir, es un ángulo recto). Los otros dos ángulos son agudos (menores de 90 grados).

2. ¿Cuál es la diferencia entre la hipotenusa y los catetos?

La hipotenusa es el lado más largo de un triángulo rectángulo y se encuentra opuesto al ángulo recto. Los catetos son los otros dos lados del triángulo que forman el ángulo recto.

3. ¿Cómo se puede verificar el teorema de Pitágoras?

Se puede verificar el teorema de Pitágoras midiendo los lados de un triángulo rectángulo y comprobando que la fórmula a² + b² = c² se cumple.

4. ¿Qué es un caso especial del teorema de Pitágoras?

Un caso especial del teorema de Pitágoras se produce cuando uno de los catetos mide la mitad de la longitud de la hipotenusa. En este caso, los tres lados del triángulo forman un triángulo isósceles rectángulo.

5. ¿Por qué es importante el teorema de Pitágoras?

El teorema de Pitágoras es importante porque es utilizado en una gran variedad de situaciones en la vida cotidiana, desde la construcción de edificios hasta la medición de distancias y la resolución de problemas matemáticos. Además, el teorema es un concepto fundamental en la geometría y es utilizado en muchas áreas de las matemáticas.