Descubre el teorema clave de la geometría en este artículo

La geometría es una rama de las matemáticas que estudia las formas, tamaños y posiciones relativas de los objetos en el espacio. Desde la antigua Grecia, la geometría ha sido una herramienta fundamental para la resolución de problemas científicos y tecnológicos, además de ser una fuente de inspiración para artistas y diseñadores. En este artículo, te presentaremos el teorema clave de la geometría, que ha sido una piedra angular en el desarrollo de esta disciplina.

¿Qué es un teorema?

Antes de adentrarnos en el teorema clave de la geometría, es importante entender qué es un teorema. Un teorema es una afirmación que se puede demostrar de manera rigurosa y que se considera verdadera. En la geometría, los teoremas se basan en axiomas o proposiciones que se aceptan como verdaderas sin necesidad de demostración.

El teorema de Pitágoras

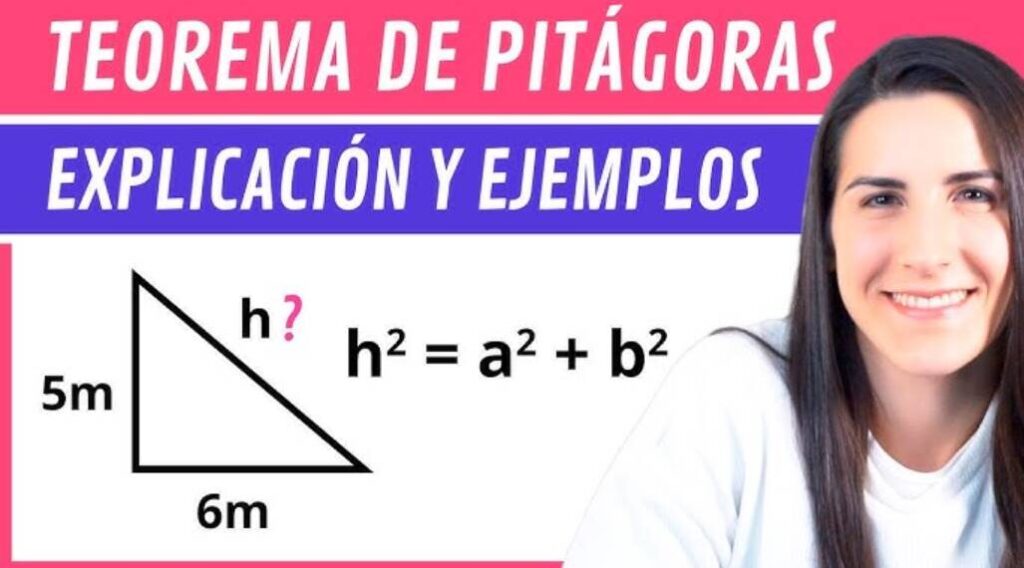
El teorema de Pitágoras es uno de los teoremas más conocidos de la geometría. Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los catetos (los otros dos lados). Este teorema tiene una amplia variedad de aplicaciones, desde la medición de la distancia entre ciudades hasta la construcción de edificios y puentes.

El teorema de Euclides

Otro teorema importante de la geometría es el teorema de Euclides, también conocido como el teorema fundamental de la geometría. Este teorema establece que si dos triángulos tienen dos lados y el ángulo incluido iguales, entonces los triángulos son congruentes. Esto significa que tienen la misma forma y tamaño, aunque puedan estar situados en posiciones diferentes.

El teorema clave de la geometría

El teorema clave de la geometría es el teorema de Tales. Este teorema establece que si dos rectas paralelas son cortadas por una tercera recta (transversal), entonces los segmentos resultantes son proporcionales. Es decir, si dividimos cualquiera de los segmentos por su segmento correspondiente en la otra recta, el resultado es el mismo para todos los segmentos.

Este teorema es fundamental en la geometría porque permite calcular longitudes y áreas en figuras geométricas complejas. Por ejemplo, si tenemos un triángulo y trazamos una recta paralela a uno de sus lados, podemos usar el teorema de Tales para calcular la longitud de otro lado o la altura del triángulo.

Aplicaciones del teorema de Tales

El teorema de Tales tiene una amplia variedad de aplicaciones en la geometría y en la vida cotidiana. Algunas de las aplicaciones más comunes son:

• Medición de distancias inaccesibles: si tenemos dos objetos de diferentes alturas y no podemos medir directamente la distancia entre ellos, podemos usar el teorema de Tales para calcularla.
• Construcción de edificios y puentes: los arquitectos y los ingenieros utilizan el teorema de Tales para calcular las dimensiones de los edificios y puentes.
• Cálculo de áreas: el teorema de Tales permite calcular el área de figuras geométricas complejas como los trapecios y los paralelogramos.
• Optimización de procesos: en la industria y la logística, el teorema de Tales se utiliza para optimizar el uso del espacio y los recursos.

Conclusión

El teorema clave de la geometría es el teorema de Tales, que establece que si dos rectas paralelas son cortadas por una tercera recta (transversal), entonces los segmentos resultantes son proporcionales. Este teorema es fundamental en la geometría y tiene una amplia variedad de aplicaciones en la vida cotidiana y en la industria. Aprender y comprender el teorema de Tales es esencial para cualquier persona interesada en la geometría y en el mundo que nos rodea.

Preguntas frecuentes

¿Quién descubrió el teorema de Tales?

El teorema de Tales fue descubierto por Tales de Mileto, un filósofo y matemático griego del siglo VI a.C.

¿Qué es una recta transversal?

Una recta transversal es una recta que corta a dos o más rectas en diferentes puntos.

¿Qué es la proporcionalidad?

La proporcionalidad es una relación entre dos o más cantidades que se mantienen en una relación constante. En el caso del teorema de Tales, los segmentos obtenidos al cortar dos rectas paralelas con una transversal son proporcionales.

¿Cómo se aplica el teorema de Tales en la vida cotidiana?

El teorema de Tales se aplica en la medición de distancias inaccesibles, la construcción de edificios y puentes, el cálculo de áreas y la optimización de procesos en la industria y la logística.

¿Qué otros teoremas importantes hay en la geometría?

Además del teorema de Tales, hay otros teoremas importantes en la geometría como el teorema de Pitágoras, el teorema de Euclides y el teorema de Thales.