Descubre el significado de la U hacia abajo en conjuntos

Si alguna vez te has encontrado con el símbolo de la U hacia abajo en conjuntos y no sabes qué significa, no te preocupes, no eres el único. Este símbolo es utilizado en matemáticas para representar la unión de conjuntos. En este artículo, te explicaremos detalladamente qué es la unión de conjuntos y cómo usar la U hacia abajo en tus operaciones matemáticas.

¿Qué es la unión de conjuntos?

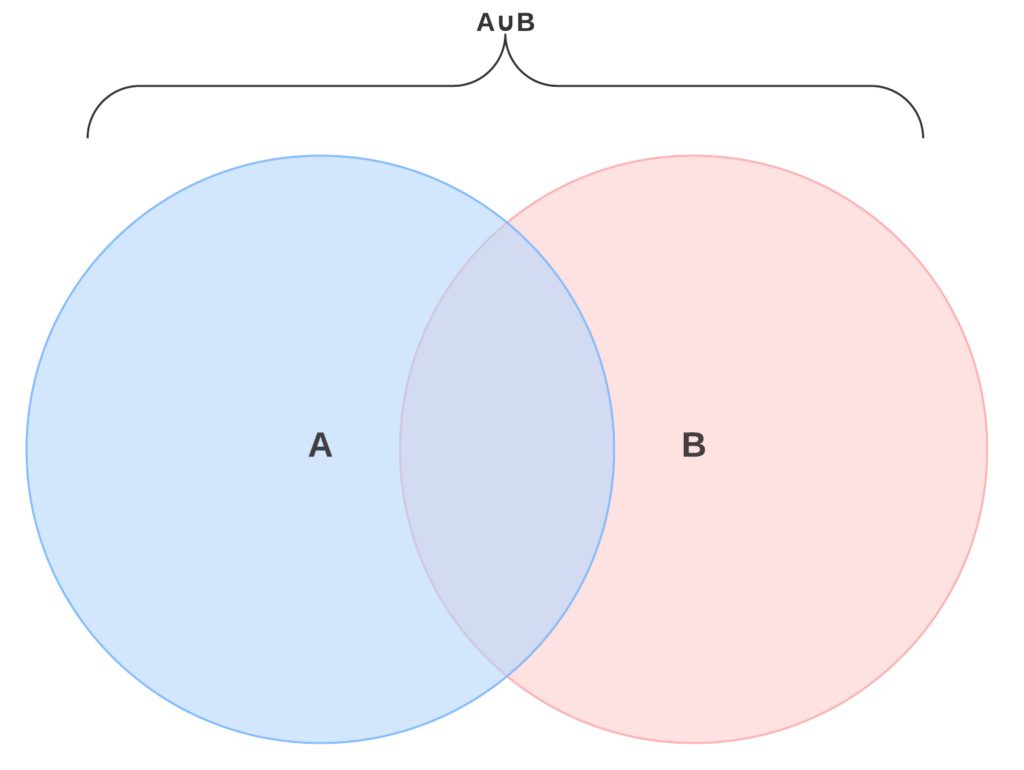
La unión de conjuntos es una operación matemática que se utiliza para combinar dos conjuntos en uno solo. La unión de dos conjuntos A y B se representa con el símbolo U hacia abajo y se define como el conjunto que contiene todos los elementos que están en A o en B, o en ambos conjuntos. En otras palabras, la unión de dos conjuntos es el conjunto que contiene todos los elementos que pertenecen a al menos uno de los dos conjuntos.

Ejemplo:

Supongamos que tenemos dos conjuntos, A y B:

A = {1, 2, 3, 4}

B = {3, 4, 5, 6}

La unión de A y B se denota con la U hacia abajo y se escribe como:

A U B = {1, 2, 3, 4, 5, 6}

Como podemos observar, la unión de A y B contiene todos los elementos de A y B, sin repetir ningún elemento.

Cómo usar la U hacia abajo en conjuntos

Para utilizar la U hacia abajo en conjuntos, debemos seguir los siguientes pasos:

1. Identificar los conjuntos que queremos unir.

2. Escribir los conjuntos separados por la U hacia abajo.

3. Eliminar los elementos repetidos en el conjunto unido.

4. Escribir el conjunto unido sin elementos repetidos.

Ejemplo:

Supongamos que queremos unir los conjuntos A = {1, 2, 3, 4} y B = {3, 4, 5, 6}. Siguiendo los pasos antes mencionados, tenemos:

1. Identificamos los conjuntos A y B que queremos unir.

2. Escribimos los conjuntos separados por la U hacia abajo: A U B.

3. Eliminamos los elementos repetidos: 1, 2, 3, 4, 5, 6.

4. Escribimos el conjunto unido sin elementos repetidos: {1, 2, 3, 4, 5, 6}.

Propiedades de la unión de conjuntos

La unión de conjuntos tiene las siguientes propiedades:

1. Conmutativa: La unión de dos conjuntos es igual, independientemente del orden en que se unan.

A U B = B U A

2. Asociativa: La unión de tres o más conjuntos es igual, independientemente del orden en que se unan.

(A U B) U C = A U (B U C)

3. Identidad: La unión de un conjunto con el conjunto vacío es igual al conjunto original.

A U ∅ = A

4. Absorción: La unión de un conjunto con su complemento es igual al conjunto universal.

A U A' = U

Conclusiones

La unión de conjuntos es una operación matemática muy importante en el estudio de la teoría de conjuntos. Se utiliza para combinar dos o más conjuntos en uno solo y se representa con el símbolo de la U hacia abajo. La unión de conjuntos tiene propiedades conmutativas, asociativas, de identidad y de absorción que facilitan su uso en las operaciones matemáticas.

Preguntas frecuentes

1. ¿Qué significa la U hacia abajo en matemáticas?

La U hacia abajo es un símbolo utilizado en matemáticas para representar la unión de conjuntos. Se utiliza para combinar dos o más conjuntos en uno solo.

2. ¿Cómo se lee la U hacia abajo en matemáticas?

La U hacia abajo se lee como "unión". Por ejemplo, A U B se lee como "la unión de A y B".

3. ¿Qué es la unión de conjuntos?

La unión de conjuntos es una operación matemática que se utiliza para combinar dos o más conjuntos en uno solo. La unión de dos conjuntos se define como el conjunto que contiene todos los elementos que están en al menos uno de los dos conjuntos.

4. ¿Cuál es la propiedad de la unión de conjuntos?

La unión de conjuntos tiene propiedades conmutativas, asociativas, de identidad y de absorción.

5. ¿Para qué se utiliza la unión de conjuntos?

La unión de conjuntos se utiliza en matemáticas para combinar dos o más conjuntos en uno solo y para realizar operaciones matemáticas con conjuntos.