Descubre el significado de la infinita derivabilidad en matemáticas

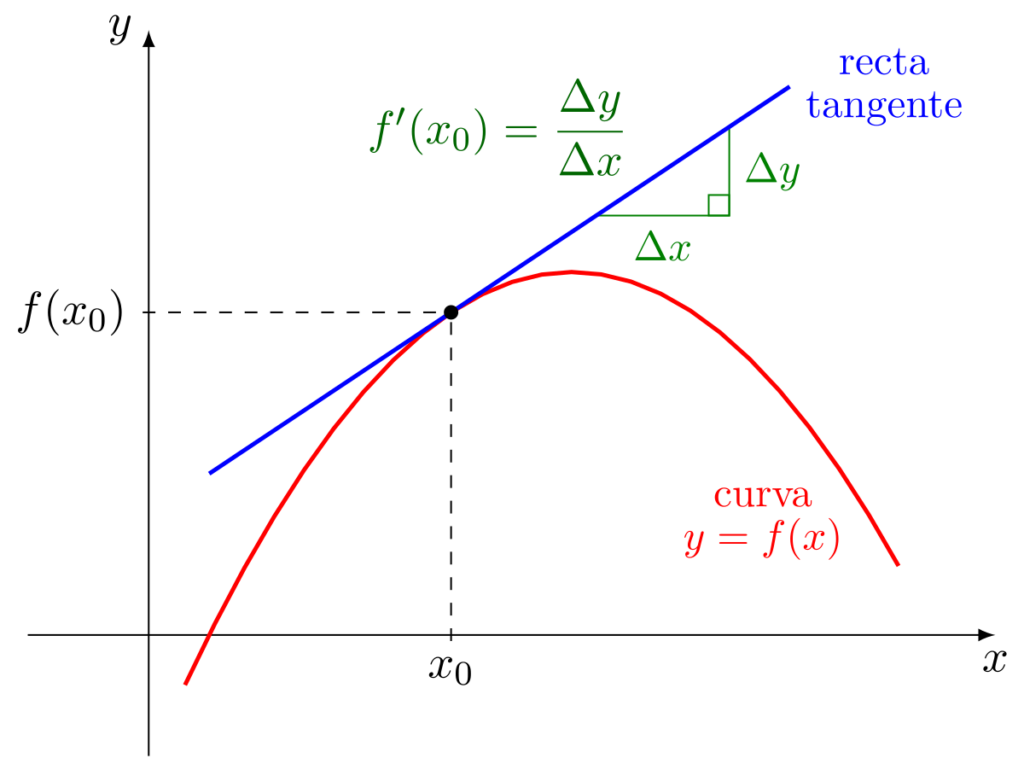
La derivada es una herramienta fundamental en matemáticas que nos permite medir la tasa de cambio de una función en un punto. Pero ¿qué pasa cuando aplicamos la derivada repetidamente? Esto nos lleva al concepto de infinita derivabilidad, que puede ser un poco confuso al principio. En este artículo, exploraremos qué significa exactamente la infinita derivabilidad y cómo se aplica en matemáticas.

¿Qué es la derivada?

Antes de adentrarnos en el concepto de infinita derivabilidad, es importante entender qué es la derivada. La derivada de una función es la tasa de cambio instantánea de dicha función en un punto. En otras palabras, nos dice cuánto cambia la función en un punto específico. Se representa por la letra "f prima" o f'.

Por ejemplo, si tenemos la función f(x) = x², la derivada de f(x) en cualquier punto x es f'(x) = 2x. Esto nos dice que la tasa de cambio instantánea de f(x) en cualquier punto x es igual a 2x.

¿Qué es la infinita derivabilidad?

La infinita derivabilidad se refiere a la capacidad de una función de ser derivada un número infinito de veces. Es decir, podemos obtener la derivada de una función, y luego la derivada de esa derivada, y así sucesivamente, un número infinito de veces.

En términos matemáticos, una función f(x) es infinitamente derivable si todas sus derivadas existen y son continuas en todo el dominio de la función.

Ejemplo de función infinitamente derivable

Un ejemplo de función infinitamente derivable es la función exponencial, f(x) = e^x. Si tomamos la primera derivada de esta función, obtenemos f'(x) = e^x. Si tomamos la segunda derivada, obtenemos f''(x) = e^x. Y si seguimos derivando, siempre obtendremos e^x. Por lo tanto, la función exponencial es infinitamente derivable.

Ejemplo de función no infinitamente derivable

Un ejemplo de función que no es infinitamente derivable es la función valor absoluto, f(x) = |x|. Si tomamos la primera derivada de esta función, obtenemos f'(x) = x/|x|. Pero si tratamos de tomar la segunda derivada, nos encontramos con un problema. En x=0, la función no tiene derivada definida, ya que la función cambia de dirección en ese punto.

Aplicaciones de la infinita derivabilidad

La infinita derivabilidad tiene aplicaciones en varios campos, incluyendo la física y la ingeniería. Por ejemplo, en la física, la aceleración es la segunda derivada de la posición con respecto al tiempo. Si una función es infinitamente derivable, podemos encontrar todas las derivadas necesarias para describir su comportamiento físico.

En la ingeniería, la infinita derivabilidad se utiliza en el análisis y diseño de sistemas de control. Los sistemas de control se basan en la medición de la tasa de cambio de una variable, por lo que es importante poder derivar las funciones que describen el comportamiento del sistema.

Conclusión

La infinita derivabilidad es un concepto importante en matemáticas que se refiere a la capacidad de una función de ser derivada un número infinito de veces. Las funciones infinitamente derivables tienen aplicaciones en la física y la ingeniería, entre otros campos. Es importante entender este concepto para comprender mejor la teoría de las funciones y su aplicación en el mundo real.

Preguntas frecuentes

¿Cómo se representa la derivada de una función?

La derivada de una función se representa por la letra "f prima" o f', y se lee como "f prima de x" o "f prima evaluada en x".

¿Qué es la tasa de cambio instantánea?

La tasa de cambio instantánea es la cantidad que una función cambia en un punto específico. La derivada de una función nos da la tasa de cambio instantánea en ese punto.

¿Por qué es importante la infinita derivabilidad en la física?

La infinita derivabilidad es importante en la física porque muchas variables físicas, como la posición y la velocidad, están relacionadas mediante derivadas. Si una función no es infinitamente derivable, puede ser difícil describir su comportamiento físico.

¿Qué es la segunda derivada?

La segunda derivada de una función es la derivada de la derivada de la función. Es decir, si tomamos la primera derivada de una función y luego la derivamos de nuevo, obtenemos la segunda derivada.

¿Qué es un sistema de control?

Un sistema de control es un sistema que se utiliza para mantener una variable en un valor deseado. Por ejemplo, un termostato es un sistema de control que mantiene la temperatura de una habitación en un valor deseado. Los sistemas de control se basan en la medición de la tasa de cambio de una variable, por lo que es importante poder derivar las funciones que describen el comportamiento del sistema.