Descubre el poder del teorema de Morgan en Algebra Booleana
El álgebra booleana es una rama de la matemática que tiene aplicaciones en informática, electrónica y telecomunicaciones. Se basa en dos valores lógicos: verdadero y falso, o 1 y 0. En este artículo, hablaremos sobre el teorema de Morgan, una herramienta importante en álgebra booleana.
¿Qué es el teorema de Morgan?
El teorema de Morgan establece que la negación de una conjunción es igual a la disyunción de las negaciones de las proposiciones y que la negación de una disyunción es igual a la conjunción de las negaciones de las proposiciones. En otras palabras, si tenemos dos proposiciones A y B, entonces:
- La negación de la conjunción de A y B es igual a la disyunción de la negación de A y la negación de B.
- La negación de la disyunción de A y B es igual a la conjunción de la negación de A y la negación de B.
¿Cómo se aplica el teorema de Morgan?
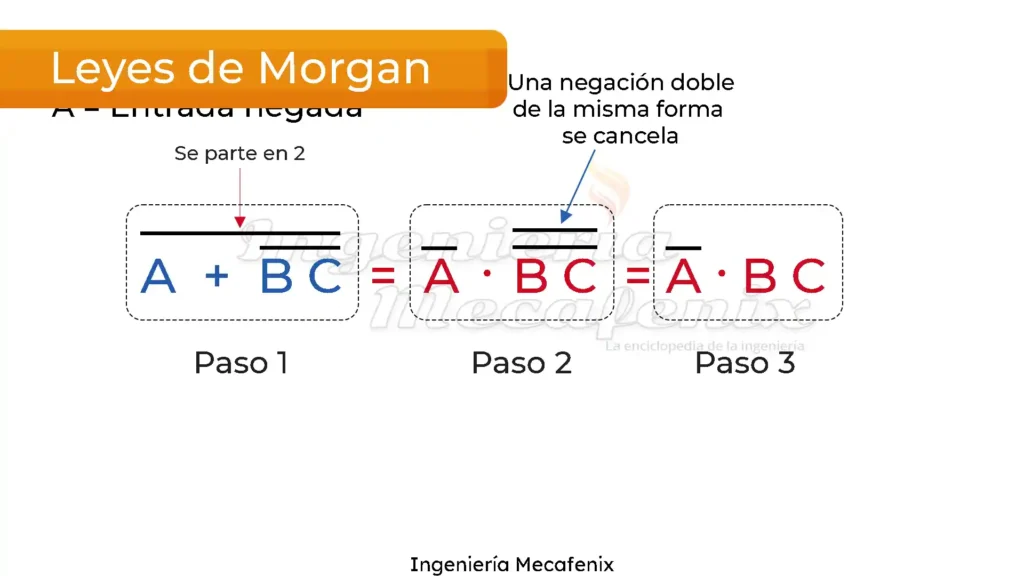
El teorema de Morgan se aplica en álgebra booleana para simplificar expresiones lógicas. Por ejemplo, si tenemos la expresión lógica ~(A ∧ B), podemos aplicar el teorema de Morgan para obtener ~(A) ∨ ~(B). De esta manera, podemos simplificar la expresión y hacerla más fácil de entender.
Ejemplos de aplicación del teorema de Morgan
Veamos algunos ejemplos de cómo se aplica el teorema de Morgan en álgebra booleana:
- Ejemplo 1: Simplificar la expresión lógica ~(A ∧ B ∨ C)
Primero, aplicamos el teorema de Morgan a la conjunción de A y B para obtener ~(A) ∨ ~(B). Luego, aplicamos la disyunción a la negación de A y B para obtener ~(A) ∨ ~(B) ∨ ~(C). Por lo tanto, la expresión simplificada es ~(A ∧ B ∨ C) = ~(A) ∨ ~(B) ∨ ~(C).
- Ejemplo 2: Simplificar la expresión lógica ~(A ∨ B ∧ C)
Primero, aplicamos el teorema de Morgan a la conjunción de B y C para obtener ~(B) ∨ ~(C). Luego, aplicamos la disyunción a la negación de A y la negación de B y C para obtener ~(A ∨ B ∧ C) = ~(A) ∨ ~(B) ∨ ~(C).
Conclusiones
El teorema de Morgan es una herramienta muy útil en álgebra booleana para simplificar expresiones lógicas. Con su aplicación, podemos hacer que las expresiones sean más fáciles de entender y trabajar con ellas. Además, el teorema de Morgan también tiene aplicaciones en informática, electrónica y telecomunicaciones.
Preguntas frecuentes
1. ¿Por qué es importante el teorema de Morgan en álgebra booleana?
El teorema de Morgan es importante en álgebra booleana porque nos permite simplificar expresiones lógicas y hacerlas más fáciles de entender y trabajar con ellas.
2. ¿Cómo se aplica el teorema de Morgan en informática?
El teorema de Morgan tiene aplicaciones en informática para simplificar expresiones lógicas en programación y diseño de circuitos electrónicos.
3. ¿Qué es una conjunción en álgebra booleana?
Una conjunción en álgebra booleana es una operación lógica que se representa con el símbolo ∧ y que significa "y". Por ejemplo, si tenemos las proposiciones A y B, la conjunción de A y B se escribe como A ∧ B.
4. ¿Qué es una disyunción en álgebra booleana?
Una disyunción en álgebra booleana es una operación lógica que se representa con el símbolo ∨ y que significa "o". Por ejemplo, si tenemos las proposiciones A y B, la disyunción de A y B se escribe como A ∨ B.
5. ¿Qué es la negación en álgebra booleana?
La negación en álgebra booleana es una operación lógica que se representa con el símbolo ~ o ¬ y que significa "no". Por ejemplo, si tenemos la proposición A, la negación de A se escribe como ~A o ¬A.
Deja una respuesta