Descubre el poder de la lógica con Álgebra Booleana SIG

La lógica es una herramienta clave en la resolución de problemas en muchas áreas, desde la informática hasta la ingeniería y la ciencia. Una rama de la lógica que se ha vuelto cada vez más importante en el mundo de la tecnología es el Álgebra Booleana SIG. En este artículo, exploraremos qué es el Álgebra Booleana SIG, cómo se utiliza y por qué es importante.

¿Qué es el Álgebra Booleana SIG?

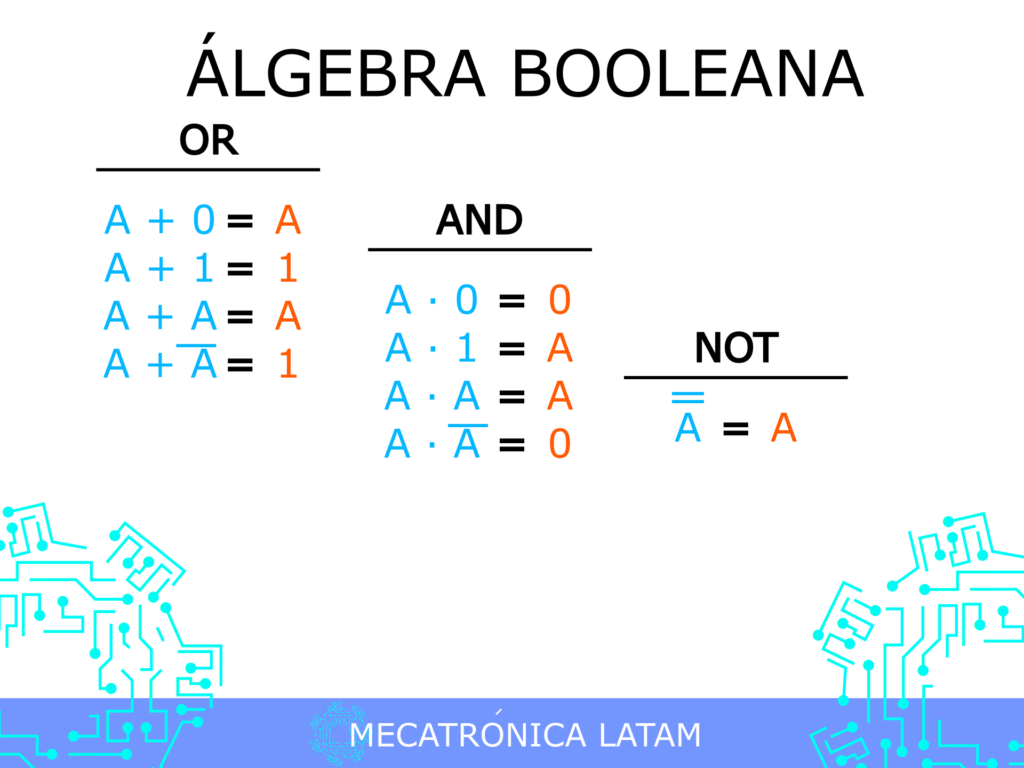
El Álgebra Booleana SIG es una rama de la lógica que se utiliza para describir y analizar los sistemas digitales. Utiliza dos valores lógicos, verdadero y falso, para representar los estados de los componentes digitales. Estos valores son a menudo representados por 1 y 0, respectivamente.

El Álgebra Booleana SIG se basa en las leyes de la lógica booleana, que establecen las reglas para la combinación de estos valores lógicos. Estas leyes incluyen la ley de identidad, la ley de doble negación, la ley de conmutatividad, la ley de asociatividad, la ley de distributividad y la ley de absorción. Al aplicar estas leyes, los ingenieros pueden diseñar y analizar sistemas digitales complejos.

¿Cómo se utiliza el Álgebra Booleana SIG?

El Álgebra Booleana SIG se utiliza en una amplia variedad de aplicaciones, desde el diseño de circuitos electrónicos hasta la programación de computadoras y la inteligencia artificial. Un ejemplo común de su uso es en la creación de tablas de verdad, que muestran todas las combinaciones posibles de valores lógicos para un conjunto de entradas.

Otra aplicación común del Álgebra Booleana SIG es en la simplificación de ecuaciones booleanas. Al reducir una ecuación booleana a su forma más simple, los ingenieros pueden diseñar sistemas más eficientes y económicos. Esto se logra mediante la aplicación de las leyes de la lógica booleana y la eliminación de términos redundantes.

¿Por qué es importante el Álgebra Booleana SIG?

El Álgebra Booleana SIG es importante porque permite a los ingenieros diseñar y analizar sistemas digitales complejos de manera efectiva y eficiente. Al utilizar las leyes de la lógica booleana, los ingenieros pueden simplificar ecuaciones booleanas y crear tablas de verdad para entender el comportamiento de los sistemas digitales.

Además, el Álgebra Booleana SIG es esencial para la programación de computadoras y la inteligencia artificial. Los algoritmos utilizados en estas áreas a menudo se basan en la lógica booleana y el Álgebra Booleana SIG para tomar decisiones y realizar cálculos.

Conclusión

El Álgebra Booleana SIG es una herramienta poderosa para el diseño y análisis de sistemas digitales. Al utilizar las leyes de la lógica booleana, los ingenieros pueden crear tablas de verdad y simplificar ecuaciones booleanas para diseñar sistemas más eficientes y económicos. Además, el Álgebra Booleana SIG es esencial para la programación de computadoras y la inteligencia artificial.

Preguntas frecuentes

¿Qué es la lógica booleana?

La lógica booleana es una rama de la lógica que utiliza dos valores lógicos, verdadero y falso, para representar los estados de los componentes digitales. Estos valores son a menudo representados por 1 y 0, respectivamente.

¿Qué es una tabla de verdad?

Una tabla de verdad es una tabla que muestra todas las combinaciones posibles de valores lógicos para un conjunto de entradas. Se utiliza para entender el comportamiento de los sistemas digitales y para simplificar ecuaciones booleanas.

¿Qué es una ecuación booleana?

Una ecuación booleana es una expresión matemática que utiliza operadores booleanos, como AND, OR y NOT, para describir el comportamiento de un sistema digital.

¿Cómo se utiliza el Álgebra Booleana SIG en la programación de computadoras?

El Álgebra Booleana SIG se utiliza en la programación de computadoras para tomar decisiones y realizar cálculos. Los algoritmos utilizados a menudo se basan en la lógica booleana y el Álgebra Booleana SIG para realizar estas tareas.

¿Por qué es importante simplificar ecuaciones booleanas?

Es importante simplificar ecuaciones booleanas porque permite a los ingenieros diseñar sistemas más eficientes y económicos. Al eliminar términos redundantes, se reducen los costos y se mejora el rendimiento del sistema.