Descubre el poder de la álgebra booleana en la informática

La informática es una disciplina que se centra en el estudio de los sistemas de información y su aplicación en diversos ámbitos. Una de las herramientas más importantes en este campo es el álgebra booleana, que nos permite realizar operaciones lógicas con valores binarios y representa la base de la electrónica digital. En este artículo, descubriremos el poder de la álgebra booleana en la informática.

¿Qué es el álgebra booleana?

El álgebra booleana es un sistema matemático que se utiliza para el análisis y diseño de circuitos electrónicos digitales. Fue desarrollada por George Boole en el siglo XIX y se basa en la lógica binaria, es decir, en la representación de los valores como 0 y 1. Esta herramienta se utiliza para realizar operaciones lógicas con valores binarios y es fundamental para la programación de computadoras y otros sistemas digitales.

¿Cómo funciona el álgebra booleana?

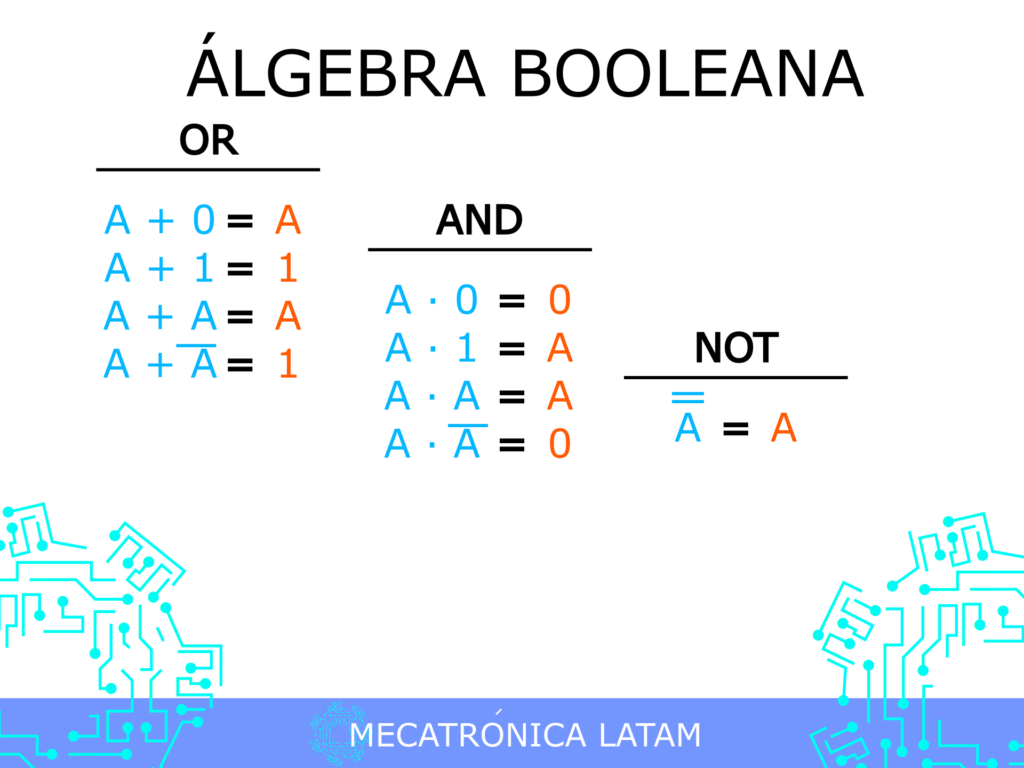
El álgebra booleana se basa en tres operaciones fundamentales: la negación, la conjunción y la disyunción. Estas operaciones se realizan con valores binarios (0 o 1) y permiten construir circuitos lógicos y programar sistemas digitales.

La negación es una operación unaria que cambia el valor de una entrada. Por ejemplo, la negación de 1 es 0 y la negación de 0 es 1.

La conjunción es una operación binaria que devuelve 1 sólo si ambas entradas son 1. Si alguna de las entradas es 0, el resultado será 0.

La disyunción es una operación binaria que devuelve 0 sólo si ambas entradas son 0. Si alguna de las entradas es 1, el resultado será 1.

¿Por qué es importante el álgebra booleana?

El álgebra booleana es fundamental en la electrónica digital y la informática, ya que permite diseñar circuitos lógicos y programar sistemas digitales. Esto se debe a que los circuitos electrónicos digitales funcionan con señales binarias (0 y 1) que se pueden manipular mediante operaciones lógicas. Por lo tanto, el álgebra booleana es la base de la programación de computadoras y otros sistemas digitales.

Aplicaciones de la álgebra booleana en la informática

El álgebra booleana tiene numerosas aplicaciones en la informática. Algunas de las más importantes son:

- Diseño de circuitos electrónicos digitales: El álgebra booleana se utiliza en el diseño de circuitos electrónicos digitales, como los procesadores, las memorias y los dispositivos de entrada y salida.

- Programación de computadoras: El álgebra booleana es la base de la programación de computadoras, ya que permite realizar operaciones lógicas con valores binarios.

- Criptografía: La criptografía es el estudio de técnicas para proteger la información mediante el cifrado. El álgebra booleana se utiliza en la criptografía para diseñar algoritmos de cifrado y descifrado.

- Redes de computadoras: El álgebra booleana se utiliza en la teoría de redes de computadoras para analizar y diseñar protocolos de comunicación.

Ejemplo de aplicación del álgebra booleana en la informática

Un ejemplo de aplicación del álgebra booleana en la informática es el diseño de una puerta lógica AND. Esta puerta lógica devuelve 1 sólo si ambas entradas son 1. Para diseñar una puerta lógica AND, se utiliza la conjunción de dos valores binarios. Por ejemplo, si tenemos dos entradas A y B, la salida de la puerta lógica AND será:

A AND B = 1 si A = 1 y B = 1
A AND B = 0 en cualquier otro caso

Conclusión

El álgebra booleana es una herramienta fundamental en la informática y la electrónica digital. Permite realizar operaciones lógicas con valores binarios y representa la base de la programación de computadoras y otros sistemas digitales. Con el conocimiento del álgebra booleana, podemos diseñar circuitos electrónicos digitales, programar computadoras y aplicar técnicas de criptografía y teoría de redes de computadoras.

Preguntas frecuentes

¿Qué es la lógica binaria?

La lógica binaria es un sistema de representación de valores que utiliza sólo dos dígitos: 0 y 1. Este sistema se utiliza en la electrónica digital y la informática para representar señales eléctricas y realizar operaciones lógicas.

¿Qué es una puerta lógica?

Una puerta lógica es un dispositivo electrónico que realiza una operación lógica con una o más entradas y produce una salida. Las puertas lógicas se utilizan en el diseño de circuitos electrónicos digitales y en la programación de computadoras.

¿Qué es la criptografía?

La criptografía es el estudio de técnicas para proteger la información mediante el cifrado. Se utiliza en la seguridad informática para proteger los datos y la privacidad de los usuarios.

¿Qué es la teoría de redes de computadoras?

La teoría de redes de computadoras es una disciplina que se centra en el estudio de las redes de computadoras y su aplicación en diversos ámbitos. Se utiliza para analizar y diseñar protocolos de comunicación y para mejorar el rendimiento de las redes de computadoras.

¿Por qué es importante conocer el álgebra booleana en la informática?

El álgebra booleana es fundamental en la informática y la electrónica digital, ya que permite diseñar circuitos lógicos y programar sistemas digitales. Con el conocimiento del álgebra booleana, podemos entender cómo funcionan los sistemas digitales y cómo podemos diseñarlos y programarlos.