Descubre el límite del infinito positivo o negativo en matemáticas

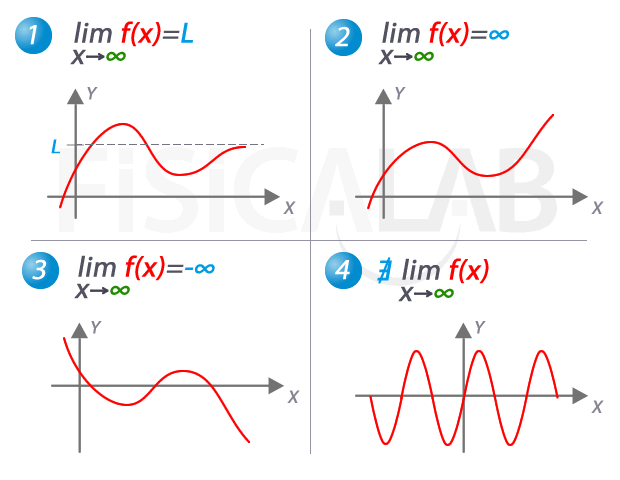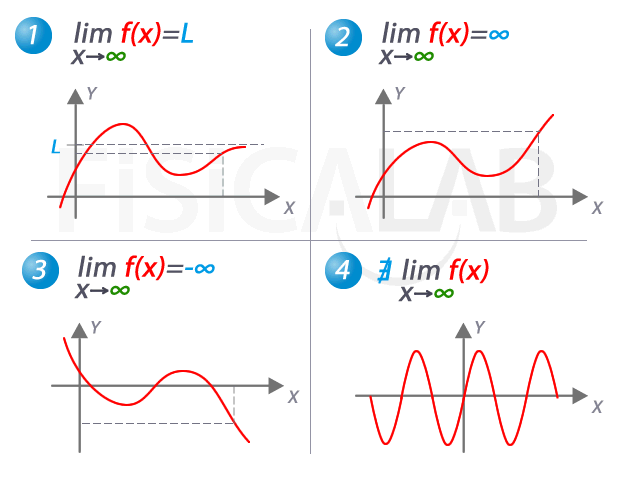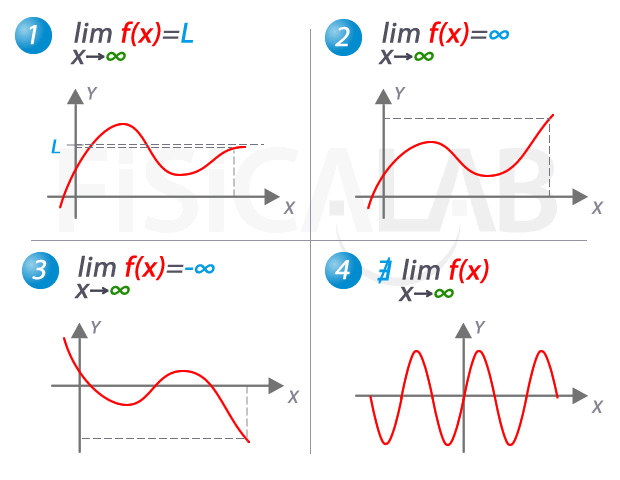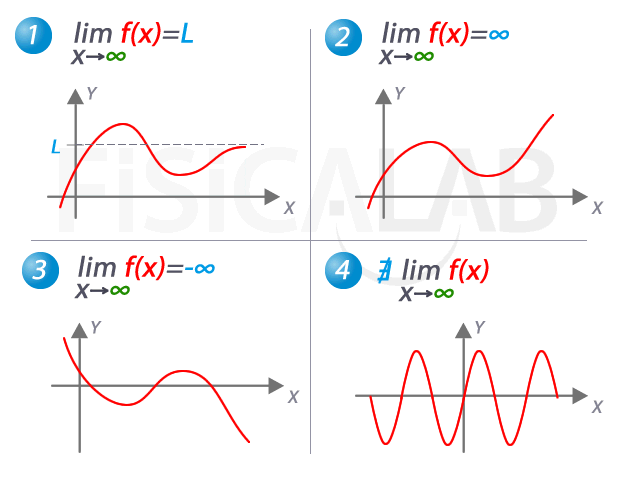
En matemáticas, el concepto de infinito se refiere a un número que no tiene un límite definido. Es un concepto abstracto que se utiliza en diversas ramas de las matemáticas, como en el cálculo y la teoría de conjuntos. En este artículo, nos centraremos en el límite del infinito positivo o negativo y cómo se calcula en matemáticas.

¿Qué es el infinito positivo o negativo?

El infinito positivo o negativo es un concepto matemático que se refiere a un número que tiende a infinito en una determinada dirección. El infinito positivo se denota con el símbolo "+∞" y se refiere a un número que tiende a infinito en la dirección positiva de la recta numérica. Por otro lado, el infinito negativo se denota con el símbolo "-∞" y se refiere a un número que tiende a infinito en la dirección negativa de la recta numérica.

Cálculo del límite del infinito positivo o negativo

El cálculo del límite del infinito positivo o negativo se basa en los siguientes principios:

Principio del límite infinito

El principio del límite infinito establece que si una función f(x) tiende a infinito en una dirección, entonces el límite de f(x) cuando x tiende a esa dirección es infinito. Es decir:

lim f(x) = +∞ o -∞

cuando x tiende a una dirección específica.

Principio de la comparación

El principio de la comparación establece que si dos funciones f(x) y g(x) se comportan de manera similar en una región alrededor del infinito, entonces el límite de f(x) cuando x tiende al infinito es igual al límite de g(x) cuando x tiende al infinito. Es decir:

lim f(x) = lim g(x)

cuando x tiende al infinito.

Ejemplos de cálculo del límite del infinito positivo o negativo

Ejemplo 1: límite de la función f(x) = x^2 cuando x tiende a +∞

Para calcular el límite de la función f(x) = x^2 cuando x tiende a +∞, podemos utilizar el principio del límite infinito. Como la función f(x) tiende a infinito cuando x tiende a +∞, entonces:

lim x^2 = +∞

cuando x tiende a +∞.

Ejemplo 2: límite de la función f(x) = 1/x cuando x tiende a 0 por la derecha

Para calcular el límite de la función f(x) = 1/x cuando x tiende a 0 por la derecha, podemos utilizar el principio de la comparación. Podemos comparar la función f(x) con la función g(x) = 1/x^2, ya que ambas funciones se acercan a infinito cuando x tiende a 0 por la derecha. Como:

lim g(x) = +∞

cuando x tiende a 0 por la derecha,

entonces:

lim f(x) = +∞

cuando x tiende a 0 por la derecha.

Conclusión

El límite del infinito positivo o negativo es un concepto matemático importante que se utiliza en diversas ramas de las matemáticas. El cálculo del límite del infinito positivo o negativo se basa en los principios del límite infinito y de la comparación, y se utiliza para determinar el comportamiento de las funciones cuando x tiende a infinito en una dirección determinada.

Preguntas frecuentes

1. ¿Qué es el límite de una función?

El límite de una función es el valor al que se acerca una función cuando la variable independiente se acerca a un determinado valor. Se utiliza para determinar el comportamiento de la función en puntos críticos, como los puntos de inflexión o los puntos de discontinuidad.

2. ¿Qué es el infinito en matemáticas?

En matemáticas, el infinito es un concepto abstracto que se utiliza para representar un número que no tiene un límite definido. Se utiliza en diversas ramas de las matemáticas, como en el cálculo y la teoría de conjuntos.

3. ¿Qué es el principio del límite infinito?

El principio del límite infinito establece que si una función tiende a infinito en una dirección, entonces el límite de esa función cuando la variable independiente tiende a esa dirección es infinito.

4. ¿Qué es el principio de la comparación?

El principio de la comparación establece que si dos funciones se comportan de manera similar en una región alrededor del infinito, entonces el límite de ambas funciones cuando la variable independiente tiende al infinito es igual.

5. ¿Por qué es importante el cálculo del límite del infinito positivo o negativo?

El cálculo del límite del infinito positivo o negativo es importante porque nos permite determinar el comportamiento de las funciones cuando la variable independiente tiende a infinito en una dirección determinada. Esto es útil para entender el comportamiento de las funciones en puntos críticos y para resolver problemas en diversas ramas de las matemáticas.