Descubre el límite de lo infinito en matemáticas

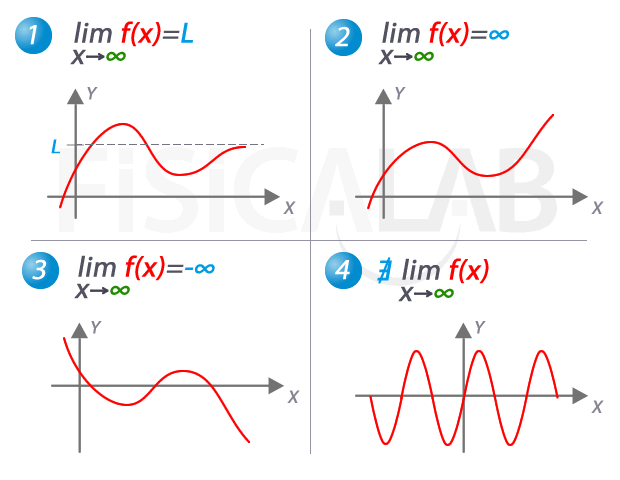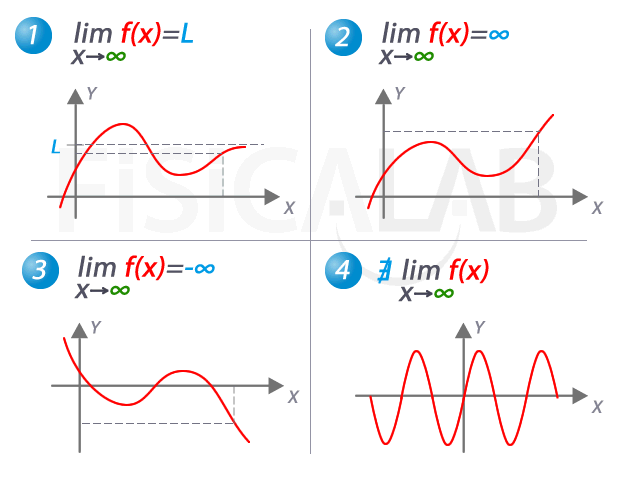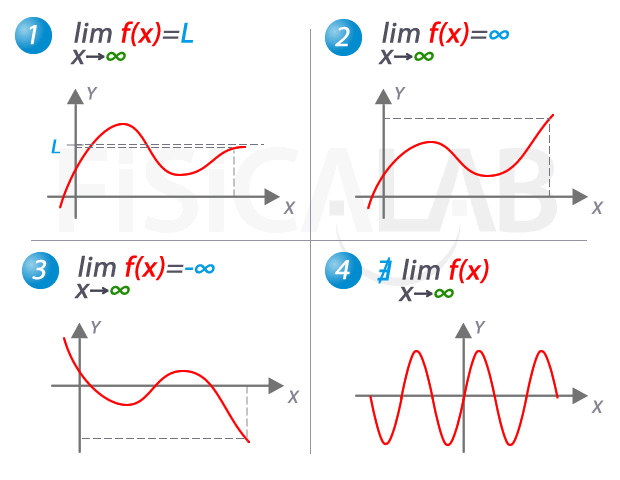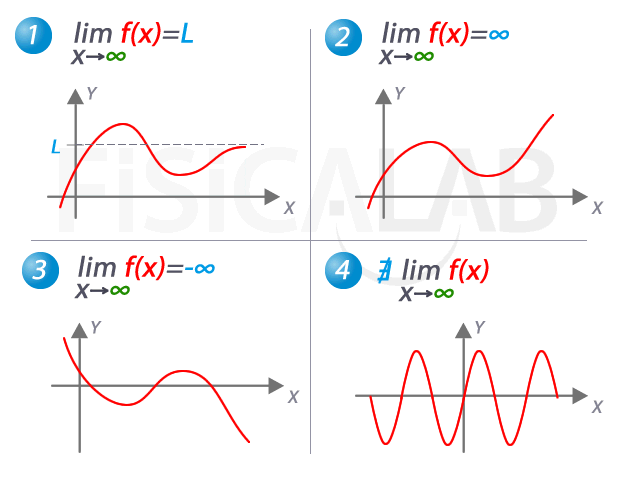
La idea de lo infinito ha sido objeto de estudio y fascinación para los matemáticos desde hace siglos. La noción de un número o una magnitud que no tiene fin ha llevado a algunos de los descubrimientos más importantes en la historia de las matemáticas. Uno de los conceptos más importantes en este campo es el límite de lo infinito.

¿Qué es el límite de lo infinito?

El límite de lo infinito se refiere a la idea de que una magnitud puede acercarse a un valor infinito sin llegar a alcanzarlo. En otras palabras, es una forma de describir el comportamiento de una función o una secuencia a medida que se acerca a un valor límite.

Para entenderlo mejor, consideremos un ejemplo simple. Supongamos que tenemos la función f(x) = 1/x. A medida que x se acerca a cero, la función se acerca a infinito. Sin embargo, nunca alcanza realmente el valor infinito. Esto se puede representar gráficamente como una línea que se acerca cada vez más a un punto sin llegar a tocarlo.

¿Por qué es importante el límite de lo infinito?

El límite de lo infinito es una herramienta esencial en la resolución de problemas matemáticos complejos. Por ejemplo, se utiliza en la definición formal del cálculo diferencial e integral, que es un pilar fundamental de las ciencias físicas y de la ingeniería. También se utiliza en la teoría de números, la geometría y la estadística, entre otros campos.

Además, el límite de lo infinito también tiene aplicaciones prácticas en la vida cotidiana. Por ejemplo, se utiliza en la modelización matemática de fenómenos naturales como la propagación de ondas en el aire o el comportamiento de los fluidos en tuberías.

¿Cómo se calcula el límite de lo infinito?

El cálculo del límite de lo infinito puede ser un proceso complejo que requiere el uso de varios métodos matemáticos. Uno de los enfoques más comunes es el uso de la regla de L'Hôpital, que permite calcular el límite de una función cuando tanto el numerador como el denominador se acercan a cero o a infinito.

Otro método común es el uso de la factorización y la simplificación algebraica para reducir la función a una forma más manejable. También se pueden utilizar técnicas de aproximación numérica, como la interpolación y la extrapolación, para estimar el valor del límite.

¿Qué aplicaciones tiene el límite de lo infinito en la vida real?

Como ya se mencionó, el límite de lo infinito tiene aplicaciones prácticas en la modelización matemática de fenómenos naturales y en la resolución de problemas en la física y la ingeniería. Pero también tiene aplicaciones en la economía, la medicina y la informática, entre otros campos.

Por ejemplo, en la economía, el límite de lo infinito se utiliza en la teoría de la oferta y la demanda para modelar el comportamiento de los mercados a medida que el número de compradores y vendedores se acerca a infinito. En la medicina, se utiliza en la modelización de la propagación de enfermedades y la predicción de su impacto en la población.

En la informática, el límite de lo infinito se utiliza en la optimización de algoritmos y la programación de sistemas de inteligencia artificial. También se utiliza en la criptografía para garantizar la seguridad de las comunicaciones en línea.

Conclusión

El límite de lo infinito es uno de los conceptos más importantes en las matemáticas y tiene aplicaciones prácticas en una amplia variedad de campos. Aunque puede ser un concepto difícil de entender, su comprensión es esencial para la resolución de problemas matemáticos complejos y para el desarrollo de nuevas tecnologías.

Preguntas frecuentes

1. ¿Qué es el límite de una función?

El límite de una función se refiere al comportamiento de la función a medida que su variable independiente se acerca a un valor determinado.

2. ¿Qué es la regla de L'Hôpital?

La regla de L'Hôpital es un método para calcular el límite de una función cuando tanto el numerador como el denominador se acercan a cero o a infinito.

3. ¿Qué aplicaciones tiene el límite de lo infinito en la economía?

El límite de lo infinito se utiliza en la teoría de la oferta y la demanda para modelar el comportamiento de los mercados a medida que el número de compradores y vendedores se acerca a infinito.

4. ¿Qué aplicaciones tiene el límite de lo infinito en la medicina?

El límite de lo infinito se utiliza en la modelización de la propagación de enfermedades y la predicción de su impacto en la población.

5. ¿Qué es la criptografía?

La criptografía es el estudio de técnicas para garantizar la seguridad de las comunicaciones en línea.