Descubre el fascinante teorema de Euler en matemáticas
Si eres un amante de las matemáticas, seguramente has escuchado hablar del teorema de Euler. Este teorema matemático es uno de los más importantes y fascinantes de la historia, y ha sido fundamental en la resolución de muchos problemas en diferentes campos de la ciencia.
En este artículo te explicaremos qué es el teorema de Euler, cómo se descubrió y cuáles son sus aplicaciones más importantes.
¿Qué es el teorema de Euler?
El teorema de Euler es una fórmula matemática que relaciona cinco de las constantes matemáticas más importantes: el número e (base de los logaritmos naturales), el número pi (constante matemática que relaciona la circunferencia de una circunferencia con su diámetro), el número imaginario i (unidad imaginaria), el número 1 (unidad real) y el número 0 (el número neutro en la suma).
La fórmula del teorema de Euler es la siguiente:
e^(i*pi) + 1 = 0
Esta fórmula puede parecer extraña e incomprensible a primera vista, pero en realidad es muy elegante y poderosa.
¿Cómo se descubrió el teorema de Euler?
El teorema de Euler fue descubierto por el matemático suizo Leonhard Euler en el siglo XVIII. Euler es considerado uno de los matemáticos más importantes de la historia, y fue el responsable de la introducción de muchos de los conceptos matemáticos que usamos hoy en día.
Euler descubrió el teorema de Euler mientras trabajaba en el campo de los números complejos. Los números complejos son números que incluyen tanto una parte real como una parte imaginaria, y son fundamentales en muchos campos de la ciencia, incluyendo la física y la ingeniería.
Euler se dio cuenta de que la fórmula e^(i*pi) tenía una propiedad muy interesante: al elevar el número e a la potencia de i por pi (el número pi multiplicado por la unidad imaginaria), el resultado era siempre igual a -1. Esta propiedad fue la base para la fórmula del teorema de Euler.
¿Cuáles son las aplicaciones del teorema de Euler?
El teorema de Euler tiene muchas aplicaciones en diferentes campos de la ciencia. Algunas de las aplicaciones más importantes del teorema de Euler incluyen:
- En la física, el teorema de Euler es fundamental para la descripción de circuitos eléctricos y electromagnéticos.
- En la ingeniería, el teorema de Euler se utiliza en la descripción de sistemas de control y en la teoría de señales.
- En la informática, el teorema de Euler es utilizado en la criptografía y en la teoría de la información.
- En la geometría, el teorema de Euler es utilizado en la descripción de poliedros y en la teoría de grafos.
¿Cómo se puede demostrar el teorema de Euler?
La demostración del teorema de Euler es bastante compleja y requiere un conocimiento profundo de matemáticas avanzadas. Sin embargo, aquí te explicamos una demostración sencilla que te ayudará a entender la idea detrás del teorema.
Primero, debemos entender la fórmula de Euler para los números complejos:
e^(ix) = cos(x) + i*sin(x)
Esta fórmula relaciona el número e elevado a la potencia de un número imaginario i por un número real x, con la suma de la función coseno y la función seno, multiplicadas por la unidad imaginaria.
Si sustituimos x por pi, la fórmula se convierte en:
e^(i*pi) = cos(pi) + i*sin(pi)
El coseno de pi es igual a -1, mientras que el seno de pi es igual a 0. Por lo tanto, podemos reescribir la fórmula como:
e^(i*pi) = -1 + 0i
Que es la misma fórmula del teorema de Euler.
Conclusión
El teorema de Euler es una de las fórmulas matemáticas más fascinantes y poderosas de la historia. Descubierto por el matemático suizo Leonhard Euler en el siglo XVIII, este teorema relaciona cinco de las constantes matemáticas más importantes y tiene muchas aplicaciones en diferentes campos de la ciencia, incluyendo la física, la ingeniería, la informática y la geometría.
La demostración del teorema de Euler es bastante compleja, pero su idea fundamental se basa en la fórmula de Euler para los números complejos.
Preguntas frecuentes
1. ¿Qué es el número imaginario?
El número imaginario es un número que se define como la raíz cuadrada de -1. Este número se representa por la letra i, y es fundamental en muchos campos de la matemática, incluyendo la geometría y la física.
2. ¿Qué es el número e?
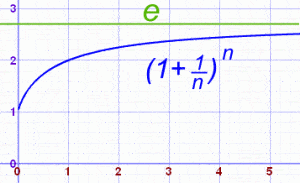
El número e es una constante matemática que se define como el límite de la sucesión (1 + 1/n)^n cuando n tiende a infinito. Este número es fundamental en muchos campos de la matemática, incluyendo el cálculo y la teoría de la probabilidad.
3. ¿Qué es el número pi?
El número pi es una constante matemática que se define como la relación entre la circunferencia de un círculo y su diámetro. Este número es fundamental en la geometría y aparece en muchas fórmulas matemáticas.
4. ¿Qué es la función coseno?
La función coseno es una función matemática que relaciona un ángulo con el coseno de ese ángulo. Esta función es fundamental en la trigonometría y aparece en muchas fórmulas matemáticas.
5. ¿Qué es la función seno?
La función seno es una función matemática que relaciona un ángulo con el seno de ese ángulo. Esta función es fundamental en la trigonometría y aparece en muchas fórmulas matemáticas.
Deja una respuesta