Descubre ejemplos claros de proposiciones simples en lógica matemática
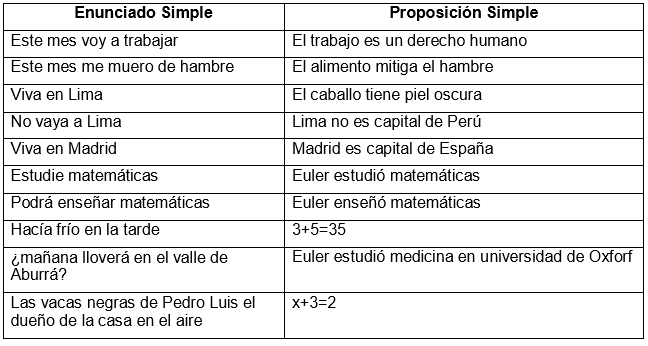
La lógica matemática es una disciplina que tiene como objetivo estudiar las leyes del razonamiento y del pensamiento. Una de las herramientas más importantes de la lógica matemática son las proposiciones simples, que son enunciados que pueden ser verdaderos o falsos. En este artículo, vamos a explorar algunos ejemplos claros de proposiciones simples en lógica matemática.
- ¿Qué son las proposiciones simples?
- Ejemplos de proposiciones simples
- Conclusión
-
Preguntas frecuentes
- 1. ¿Las proposiciones simples siempre tienen que ser verdaderas o falsas?
- 2. ¿Las proposiciones simples siempre tienen que ser matemáticas?
- 3. ¿Pueden las proposiciones simples ser complejas?
- 4. ¿Son las proposiciones simples lo mismo que las afirmaciones?
- 5. ¿Por qué son importantes las proposiciones simples en la lógica matemática?
¿Qué son las proposiciones simples?
Antes de profundizar en los ejemplos de proposiciones simples, es importante entender qué son. Una proposición simple es un enunciado que puede ser verdadero o falso, pero no ambas cosas a la vez. Por ejemplo, "2+2=4" es una proposición simple, ya que es verdadera, mientras que "2+2=5" es una proposición simple falsa, ya que es falsa.
Ejemplos de proposiciones simples
A continuación, vamos a explorar algunos ejemplos claros de proposiciones simples en lógica matemática:
1. "El cielo es azul"
Esta proposición simple es verdadera o falsa dependiendo del momento del día y de las condiciones atmosféricas. Si el cielo está despejado y el sol está brillando, la proposición es verdadera. Si el cielo está cubierto de nubes, la proposición es falsa.
2. "1 es un número par"
Esta proposición simple es falsa, ya que el número 1 es impar. Sin embargo, si la proposición hubiera sido "2 es un número par", entonces sería verdadera.
3. "10 es mayor que 5"
Esta proposición simple es verdadera, ya que 10 es mayor que 5.
4. "El agua hierve a 100 grados Celsius"
Esta proposición simple es verdadera, ya que el agua hierve a una temperatura de 100 grados Celsius al nivel del mar.
5. "El sol sale por el oeste"
Esta proposición simple es falsa, ya que el sol sale por el este y se pone por el oeste.
Conclusión
Las proposiciones simples son enunciados que pueden ser verdaderos o falsos, pero no ambas cosas a la vez. En lógica matemática, estas proposiciones son fundamentales para entender las leyes del razonamiento y del pensamiento. Los ejemplos que hemos explorado en este artículo son solo una pequeña muestra de las muchas proposiciones simples que existen en la lógica matemática.
Preguntas frecuentes
1. ¿Las proposiciones simples siempre tienen que ser verdaderas o falsas?
Sí, una proposición simple siempre debe ser verdadera o falsa, no puede ser ambas cosas a la vez.
2. ¿Las proposiciones simples siempre tienen que ser matemáticas?
No necesariamente. Las proposiciones simples pueden ser sobre cualquier cosa, desde el clima hasta la política.
3. ¿Pueden las proposiciones simples ser complejas?
No, las proposiciones simples deben ser enunciados simples que puedan ser verdaderos o falsos.
4. ¿Son las proposiciones simples lo mismo que las afirmaciones?
Sí, las proposiciones simples y las afirmaciones son sinónimos en lógica matemática.
5. ¿Por qué son importantes las proposiciones simples en la lógica matemática?
Las proposiciones simples son importantes en la lógica matemática porque son la base del razonamiento y del pensamiento lógico. Sin ellas, no podríamos hacer deducciones ni llegar a conclusiones precisas.
Deja una respuesta