Descubre dónde aplicar el teorema de Lagrange

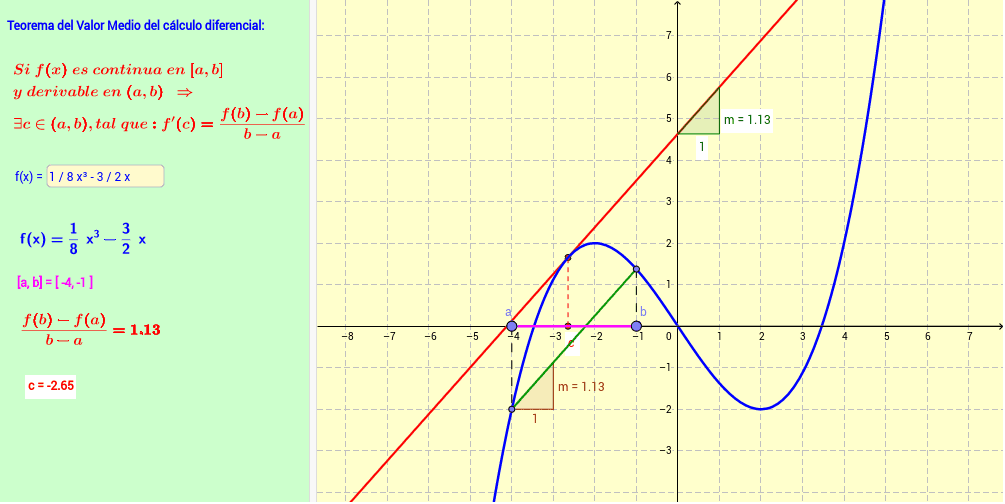
El teorema de Lagrange es una herramienta matemática poderosa que puede ser aplicada en diferentes contextos, desde la física y la ingeniería hasta la economía y la estadística. Este teorema, también conocido como el teorema del valor medio, establece que si una función es continua en un intervalo cerrado, entonces existe al menos un punto en ese intervalo en el que la derivada de la función es igual al cociente de la diferencia de las imágenes de los extremos del intervalo y la diferencia de los extremos del intervalo.

En otras palabras, el teorema de Lagrange nos permite encontrar el valor exacto de una función en un punto específico, siempre y cuando conozcamos los valores de la función en los extremos del intervalo. A continuación, te presentamos algunos de los contextos más comunes en los que se aplica el teorema de Lagrange.

1. Cálculo de máximos y mínimos

El teorema de Lagrange es una herramienta muy útil en el cálculo de máximos y mínimos de una función. Para ello, es necesario encontrar los puntos críticos de la función, es decir, los puntos en los que la derivada de la función es igual a cero o no existe. Una vez encontrados los puntos críticos, podemos aplicar el teorema de Lagrange para determinar si se trata de un máximo o un mínimo.

2. Optimización de funciones

El teorema de Lagrange también es muy útil en la optimización de funciones. En este contexto, se busca encontrar el punto en el que la función alcanza su valor máximo o mínimo, sujeto a ciertas restricciones. Por ejemplo, podemos querer maximizar el área de un rectángulo sujeto a una restricción en el perímetro. En este caso, podemos aplicar el teorema de Lagrange para encontrar el valor máximo de la función sujeto a esa restricción.

3. Análisis de curvas y trayectorias

El teorema de Lagrange también se utiliza en el análisis de curvas y trayectorias en física y en ingeniería. Por ejemplo, podemos querer encontrar el punto en el que la velocidad de un objeto alcanza su valor máximo en una trayectoria determinada. En este caso, podemos aplicar el teorema de Lagrange para encontrar el punto en el que la derivada de la velocidad es igual a cero.

4. Estudio de funciones complejas

El teorema de Lagrange también puede ser aplicado en el estudio de funciones complejas en matemáticas avanzadas. En este contexto, el teorema de Lagrange puede ser utilizado para demostrar ciertas propiedades de las funciones complejas y para resolver problemas complejos en el ámbito de la matemática pura.

Conclusión

El teorema de Lagrange es una herramienta matemática muy poderosa y versátil que puede ser aplicada en diferentes contextos, desde el cálculo de máximos y mínimos hasta el estudio de funciones complejas en matemáticas avanzadas. Si estás interesado en aprender más sobre el teorema de Lagrange y cómo aplicarlo en diferentes contextos, te recomendamos que consultes fuentes especializadas en matemáticas y física.

Preguntas frecuentes

1. ¿Qué es el teorema de Lagrange?

El teorema de Lagrange, también conocido como el teorema del valor medio, establece que si una función es continua en un intervalo cerrado, entonces existe al menos un punto en ese intervalo en el que la derivada de la función es igual al cociente de la diferencia de las imágenes de los extremos del intervalo y la diferencia de los extremos del intervalo.

2. ¿En qué contextos se aplica el teorema de Lagrange?

El teorema de Lagrange puede ser aplicado en diferentes contextos, desde el cálculo de máximos y mínimos hasta el estudio de funciones complejas en matemáticas avanzadas.

3. ¿Cómo se aplica el teorema de Lagrange en el cálculo de máximos y mínimos?

Para aplicar el teorema de Lagrange en el cálculo de máximos y mínimos, es necesario encontrar los puntos críticos de la función, es decir, los puntos en los que la derivada de la función es igual a cero o no existe. Una vez encontrados los puntos críticos, podemos aplicar el teorema de Lagrange para determinar si se trata de un máximo o un mínimo.

4. ¿Cómo se aplica el teorema de Lagrange en la optimización de funciones?

En la optimización de funciones, se busca encontrar el punto en el que la función alcanza su valor máximo o mínimo, sujeto a ciertas restricciones. En este contexto, podemos aplicar el teorema de Lagrange para encontrar el valor máximo de la función sujeto a esa restricción.

5. ¿Cómo se aplica el teorema de Lagrange en el análisis de curvas y trayectorias?

En el análisis de curvas y trayectorias, podemos aplicar el teorema de Lagrange para encontrar el punto en el que la velocidad de un objeto alcanza su valor máximo en una trayectoria determinada. En este caso, podemos aplicar el teorema de Lagrange para encontrar el punto en el que la derivada de la velocidad es igual a cero.