Descubre cuántos teoremas de Pitágoras existen

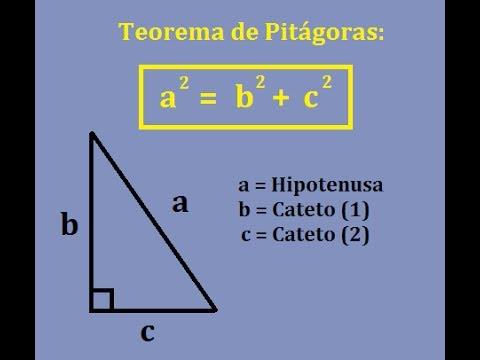
El teorema de Pitágoras es uno de los conceptos matemáticos más importantes y conocidos en todo el mundo. La fórmula a² + b² = c², que establece la relación entre los lados de un triángulo rectángulo, se ha utilizado durante miles de años para resolver problemas geométricos y matemáticos. Pero, ¿cuántos teoremas de Pitágoras existen? En este artículo, exploraremos esta pregunta y descubriremos la respuesta.

¿Qué es el teorema de Pitágoras?

Antes de hablar sobre los diferentes teoremas de Pitágoras, es importante comprender qué es exactamente el teorema original. En esencia, el teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados.

Este teorema se puede expresar matemáticamente como a² + b² = c², donde "a" y "b" son los catetos del triángulo (los lados que forman el ángulo recto) y "c" es la hipotenusa. Esta fórmula se puede utilizar para encontrar la longitud de cualquier lado de un triángulo rectángulo si se conocen las longitudes de los otros dos lados.

¿Cuántos teoremas de Pitágoras existen?

Ahora, volvamos a la pregunta original: ¿cuántos teoremas de Pitágoras existen? En realidad, hay más de uno. A lo largo de los años, los matemáticos han descubierto varias versiones del teorema original que se aplican a diferentes tipos de triángulos y situaciones.

Teorema de Pitágoras en triángulos isósceles

Uno de estos teoremas se aplica específicamente a los triángulos isósceles, que son aquellos que tienen dos lados iguales. En un triángulo isósceles rectángulo, la longitud de la hipotenusa es igual a la raíz cuadrada de dos veces la longitud de cualquiera de los catetos. Esto se puede expresar matemáticamente como c = a√2.

Teorema de Pitágoras en triángulos equiláteros

Otro teorema se aplica a los triángulos equiláteros, que tienen tres lados iguales. En un triángulo equilátero rectángulo, la longitud de la hipotenusa es igual a la raíz cuadrada de tres veces la longitud de cualquiera de los catetos. Esto se puede expresar matemáticamente como c = a√3.

Teorema de Pitágoras en triángulos escalenos

Incluso los triángulos escalenos (aquellos que no tienen lados iguales) tienen su propio teorema de Pitágoras. En un triángulo escaleno rectángulo, la longitud de la hipotenusa es igual a la raíz cuadrada de la suma de los cuadrados de los otros dos lados, menos dos veces el producto de esos lados y el coseno del ángulo entre ellos. Esto se puede expresar matemáticamente como c = √(a² + b² - 2abcosC).

Conclusión

Existen varios teoremas de Pitágoras que se aplican a diferentes tipos de triángulos y situaciones. El teorema original establece la relación entre los lados de un triángulo rectángulo, mientras que otros teoremas se aplican a triángulos isósceles, equiláteros y escalenos. Conocer estos teoremas puede ser útil en la resolución de problemas matemáticos y geométricos.

Preguntas frecuentes

¿Quién descubrió el teorema de Pitágoras?

El teorema de Pitágoras lleva el nombre del matemático griego Pitágoras, quien lo descubrió alrededor del año 500 a.C.

¿Por qué es importante el teorema de Pitágoras?

El teorema de Pitágoras es importante porque se utiliza en muchas áreas de la ciencia y las matemáticas, incluyendo la física, la ingeniería y la estadística. También es un concepto fundamental en la geometría.

¿Cómo se utiliza el teorema de Pitágoras en la vida cotidiana?

El teorema de Pitágoras se utiliza en la vida cotidiana en situaciones en las que es necesario calcular distancias, como en la construcción de edificios y la medición de terrenos.

¿Qué es un triángulo rectángulo?

Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir, un ángulo de 90 grados. Los otros dos ángulos suman 90 grados entre ellos.

¿Qué son los catetos de un triángulo?

Los catetos de un triángulo son los dos lados que forman el ángulo recto. El tercer lado se llama hipotenusa.