Descubre cuándo usar el teorema de Lagrange: ¡optimiza tus cálculos!

Si te encuentras estudiando matemáticas, es muy probable que hayas escuchado hablar del teorema de Lagrange. Este teorema es una herramienta muy útil para optimizar cálculos en diferentes áreas de las matemáticas, y en este artículo te explicaremos cuándo debes utilizarlo y cómo funciona.

¿Qué es el teorema de Lagrange?

El teorema de Lagrange, también conocido como el teorema del valor medio, es una herramienta matemática que nos permite encontrar el valor máximo o mínimo de una función en un intervalo dado. Fue desarrollado por el matemático francés Joseph-Louis Lagrange en el siglo XVIII.

¿Cómo funciona el teorema de Lagrange?

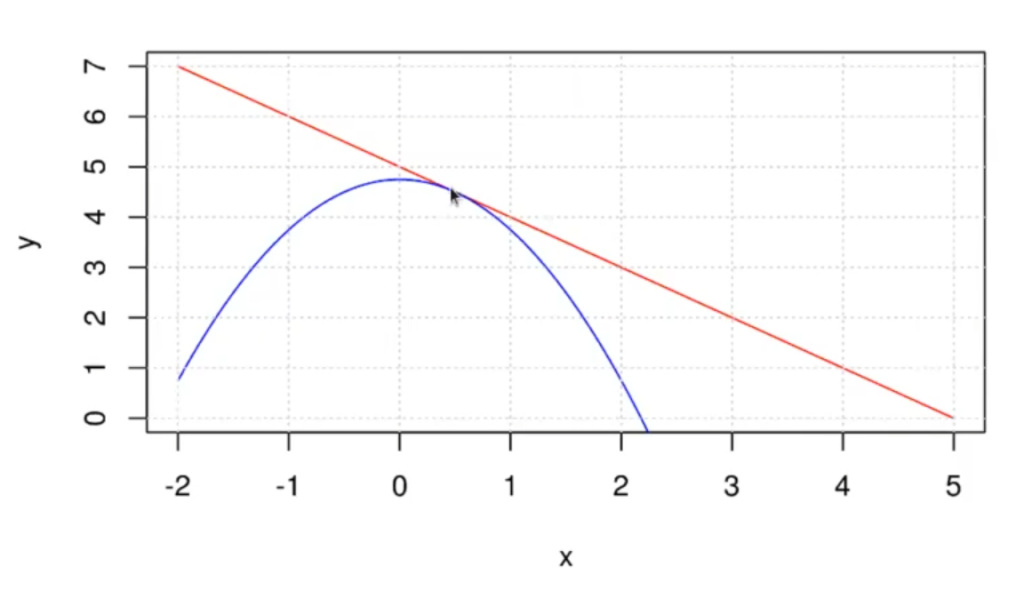
El teorema de Lagrange se basa en la idea de que si una función es continua en un intervalo cerrado y diferenciable en su interior, entonces existe al menos un punto en ese intervalo en el que la pendiente de la recta tangente a la función es igual a la pendiente de la recta secante que une los extremos del intervalo.

Matemáticamente, esto se puede expresar de la siguiente manera:

Si f(x) es una función continua en el intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b), entonces existe al menos un número c en el intervalo abierto (a, b) tal que:

f'(c) = [f(b) - f(a)] / (b - a)

Esta ecuación nos permite encontrar el valor de c, que es el punto en el que la pendiente de la recta tangente es igual a la pendiente de la recta secante.

¿Cuándo debemos utilizar el teorema de Lagrange?

El teorema de Lagrange es una herramienta muy útil para encontrar los valores máximos y mínimos de una función. En general, lo utilizamos cuando tenemos una función que queremos optimizar en un intervalo dado.

Por ejemplo, si tenemos una función que representa el costo de producción de un producto en función del número de unidades producidas, podemos utilizar el teorema de Lagrange para encontrar el número de unidades que minimiza el costo de producción.

Debemos utilizar el teorema de Lagrange cuando queremos encontrar el valor máximo o mínimo de una función en un intervalo dado.

Ejemplo de aplicación del teorema de Lagrange

Supongamos que queremos encontrar el valor mínimo de la función f(x) = x^2 + 2x en el intervalo [-1, 2].

Primero, calculamos la derivada de la función:

f'(x) = 2x + 2

Luego, planteamos la ecuación del teorema de Lagrange:

f'(c) = [f(2) - f(-1)] / (2 - (-1))

2c + 2 = (2^2 + 2(2)) - ((-1)^2 + 2(-1)) / 3

2c + 2 = 15 / 3

2c + 2 = 5

2c = 3

c = 3/2

Por lo tanto, el valor mínimo de la función f(x) en el intervalo [-1, 2] se alcanza en el punto c = 3/2.

Conclusión

El teorema de Lagrange es una herramienta muy útil para optimizar cálculos en diferentes áreas de las matemáticas. Nos permite encontrar los valores máximos y mínimos de una función en un intervalo dado, lo que tiene aplicaciones en la resolución de problemas de optimización en diferentes campos.

Preguntas frecuentes

¿Qué es la derivada de una función?

La derivada de una función es la tasa de cambio de la función en un punto dado. Se calcula como el límite de la razón incremental de la función cuando el intervalo de cambio tiende a cero.

¿Qué es una función continua?

Una función es continua si no tiene saltos ni interrupciones en su gráfica. Esto significa que la función puede ser dibujada sin levantar el lápiz del papel.

¿Qué es una función diferenciable?

Una función es diferenciable si su derivada existe en todo punto de su dominio. Esto significa que la función es suave y no tiene puntos angulares o discontinuidades en su gráfica.

¿En qué áreas se utiliza el teorema de Lagrange?

El teorema de Lagrange tiene aplicaciones en diferentes áreas de las matemáticas, como la geometría, el cálculo diferencial e integral, la física y la economía, entre otras. Se utiliza para resolver problemas de optimización en estas áreas.