Descubre cuándo aplicar el teorema de Poncelet en geometría
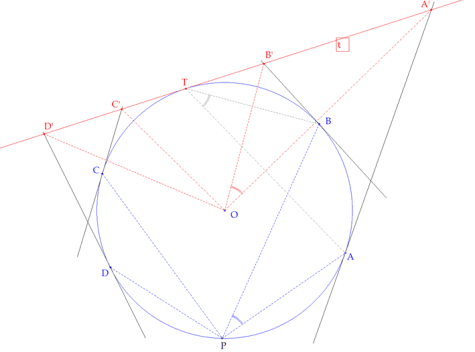
La geometría es una disciplina matemática que se encarga del estudio de las figuras y sus propiedades en el espacio. Dentro de la geometría, existen muchos teoremas y fórmulas que nos ayudan a resolver problemas y a entender mejor el mundo que nos rodea. Uno de los teoremas más importantes en geometría es el teorema de Poncelet, el cual tiene aplicaciones en diversas áreas, como la arquitectura, la ingeniería y la física. En este artículo, te explicaremos qué es el teorema de Poncelet, cuándo se aplica y cómo funciona.
¿Qué es el teorema de Poncelet?
El teorema de Poncelet fue descubierto por el matemático francés Jean-Victor Poncelet en el siglo XIX. Este teorema establece que si una figura geométrica puede ser inscrita en una circunferencia, entonces se puede trazar una circunferencia adicional que pase por los mismos puntos de la figura original y corte a la circunferencia inicial en solo un punto. En otras palabras, si una figura puede ser inscrita en una circunferencia, entonces se puede construir una circunferencia que pase por los mismos puntos de la figura y que también corte a la circunferencia inicial.
¿Cuándo se aplica el teorema de Poncelet?
El teorema de Poncelet se aplica principalmente en la geometría de dos dimensiones, y es útil para resolver problemas relacionados con figuras inscritas en circunferencias. Por ejemplo, se puede utilizar este teorema para trazar una circunferencia que pase por los mismos puntos de un triángulo, un cuadrilátero o cualquier otra figura geométrica que pueda ser inscrita en una circunferencia. Además, este teorema también tiene aplicaciones en la construcción de polígonos regulares y en la geometría proyectiva.
¿Cómo funciona el teorema de Poncelet?
El teorema de Poncelet se basa en el concepto de la geometría proyectiva, que es una rama de la geometría que estudia las propiedades de las figuras que se mantienen invariantes bajo proyecciones. En la geometría proyectiva, una proyección es una transformación que lleva los puntos de una figura en el plano a los puntos correspondientes de otra figura en el mismo plano. En el caso del teorema de Poncelet, la proyección se realiza desde la circunferencia inicial a la circunferencia adicional que se quiere construir.
Para entender mejor cómo funciona este teorema, podemos pensar en un ejemplo concreto. Supongamos que tenemos un triángulo inscrito en una circunferencia, y queremos construir una circunferencia que pase por los mismos puntos del triángulo y corte a la circunferencia inicial en un solo punto. Para hacer esto, podemos utilizar el teorema de Poncelet de la siguiente manera:
- Dibujamos una línea recta que pase por dos vértices del triángulo y el punto de corte de la circunferencia inicial.
- Extendemos esta línea recta hasta que corte a la circunferencia inicial en otro punto.
- Dibujamos una línea recta que pase por este último punto y el tercer vértice del triángulo.
- Extendemos esta línea recta hasta que corte a la circunferencia inicial en un tercer punto.
- La circunferencia buscada es la que pasa por los tres puntos obtenidos.
Conclusiones
El teorema de Poncelet es un importante resultado de la geometría que tiene aplicaciones en diversas áreas de la ciencia y la tecnología. Este teorema establece que si una figura geométrica puede ser inscrita en una circunferencia, entonces se puede trazar una circunferencia adicional que pase por los mismos puntos de la figura original y corte a la circunferencia inicial en solo un punto. El teorema de Poncelet se aplica principalmente en la geometría de dos dimensiones, y es útil para resolver problemas relacionados con figuras inscritas en circunferencias. Además, este teorema también tiene aplicaciones en la construcción de polígonos regulares y en la geometría proyectiva.
Preguntas frecuentes
1. ¿Qué es la geometría proyectiva?
La geometría proyectiva es una rama de la geometría que estudia las propiedades de las figuras que se mantienen invariantes bajo proyecciones.
2. ¿En qué áreas se aplica el teorema de Poncelet?
El teorema de Poncelet tiene aplicaciones en diversas áreas, como la arquitectura, la ingeniería y la física.
3. ¿Qué es una proyección en geometría proyectiva?
En la geometría proyectiva, una proyección es una transformación que lleva los puntos de una figura en el plano a los puntos correspondientes de otra figura en el mismo plano.
4. ¿Cómo se utiliza el teorema de Poncelet para construir una circunferencia?
Para construir una circunferencia utilizando el teorema de Poncelet, se dibuja una línea recta que pase por dos vértices de la figura y el punto de corte de la circunferencia inicial. Luego se extiende esta línea recta hasta que corte a la circunferencia inicial en otro punto, y se dibuja una línea recta que pase por este último punto y el tercer vértice de la figura. Finalmente, se extiende esta línea recta hasta que corte a la circunferencia inicial en un tercer punto, y la circunferencia buscada es la que pasa por los tres puntos obtenidos.
5. ¿Qué otras propiedades interesantes tiene la geometría proyectiva?
La geometría proyectiva tiene muchas propiedades interesantes, como la dualidad, la involución y la polaridad, que tienen aplicaciones en diversas áreas de la ciencia y la tecnología.
Deja una respuesta