Descubre cómo usar el teorema de Tales en tu día a día
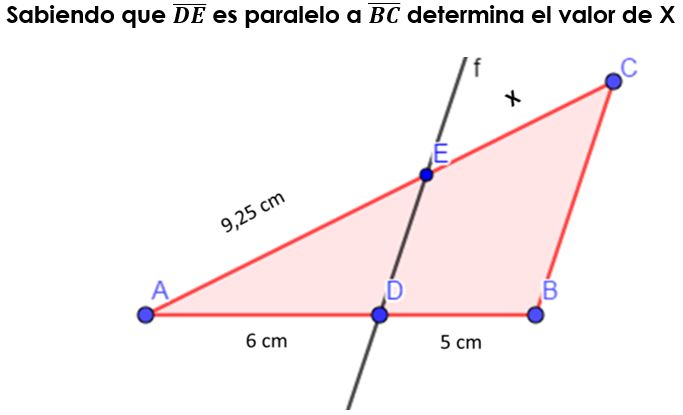
El teorema de Tales es una herramienta matemática que puede ser útil en nuestro día a día más de lo que creemos. Este teorema, nombrado en honor al matemático griego Tales de Mileto, establece una relación entre las longitudes de segmentos de líneas paralelas cortadas por una transversal. En otras palabras, si dos líneas son paralelas y una tercera línea las cruza, los segmentos que se forman tienen una relación proporcional. A continuación, te mostramos cómo puedes aplicar este teorema en situaciones cotidianas.
1. Cálculo de distancias
El teorema de Tales se puede utilizar para calcular distancias. Por ejemplo, si estás en una montaña y quieres calcular la altura de una torre, puedes medir la sombra que la torre proyecta en el suelo y la sombra que tú proyectas en el suelo. Si mides la distancia entre los dos puntos donde se proyectan las sombras, y la distancia entre el punto donde estás y el punto donde proyectas tu sombra, puedes utilizar el teorema de Tales para calcular la altura de la torre.
2. Redimensionamiento de objetos
Imagina que tienes que hacer una maqueta de un edificio y las proporciones del modelo son diferentes a las del edificio real. Puedes utilizar el teorema de Tales para redimensionar el modelo sin perder las proporciones del edificio. Si conoces las medidas del edificio real, puedes utilizar el teorema de Tales para establecer las proporciones correctas en la maqueta.
3. Cálculo de porcentajes
El teorema de Tales también se puede utilizar para calcular porcentajes. Por ejemplo, si quieres calcular el porcentaje de grasa en tu cuerpo, puedes utilizar el teorema de Tales para comparar la longitud de dos segmentos. Mide la longitud de tu brazo y la longitud de tu antebrazo. Luego, mide la longitud de la parte superior de tu brazo y la parte inferior. Si utilizas el teorema de Tales, puedes calcular el porcentaje de grasa en tu cuerpo.
4. Proporciones en la cocina
El teorema de Tales también se puede aplicar en la cocina. Por ejemplo, si quieres hacer una receta y necesitas reducir o aumentar las cantidades de los ingredientes, puedes utilizar el teorema de Tales para mantener las proporciones de los ingredientes. Si duplicas la cantidad de la receta, también duplicas la cantidad de cada ingrediente utilizando el teorema de Tales.
5. Diseño de interiores
El teorema de Tales también se puede utilizar en el diseño de interiores. Si quieres colgar una serie de cuadros en una pared, puedes utilizar el teorema de Tales para establecer la distancia entre ellos y su altura en relación con el tamaño de la pared. Utilizando el teorema de Tales, puedes asegurarte de que los cuadros estén bien proporcionados y se vean bien en la pared.
Conclusión
El teorema de Tales es una herramienta matemática que puede ser útil en muchas situaciones cotidianas. Desde el cálculo de distancias hasta el diseño de interiores, el teorema de Tales puede ayudarte a mantener proporciones precisas y a resolver problemas de manera eficiente.
Preguntas frecuentes
¿Qué es el teorema de Tales?
El teorema de Tales es una herramienta matemática que establece una relación entre las longitudes de segmentos de líneas paralelas cortadas por una transversal.
¿Quién descubrió el teorema de Tales?
El teorema de Tales fue nombrado en honor al matemático griego Tales de Mileto, quien lo descubrió.
¿En qué situaciones se puede utilizar el teorema de Tales?
El teorema de Tales se puede utilizar en situaciones cotidianas como el cálculo de distancias, el redimensionamiento de objetos, el cálculo de porcentajes, el diseño de interiores, entre otros.
¿Cómo se utiliza el teorema de Tales?
El teorema de Tales se utiliza para establecer una relación proporcional entre los segmentos que se forman al cortar dos líneas paralelas con una transversal.
¿Por qué es importante conocer el teorema de Tales?
Conocer el teorema de Tales puede ser útil en situaciones cotidianas y en la resolución de problemas de manera eficiente. Además, es una herramienta matemática básica que puede ser utilizada en otros campos de estudio.
Deja una respuesta