Descubre cómo resolver límites infinitos negativos

Los límites infinitos negativos son una de las situaciones más comunes con las que se enfrentan los estudiantes de matemáticas. Estos límites pueden ser difíciles de entender y resolver, pero con un poco de práctica y comprensión, es posible dominarlos. En este artículo, te mostraremos cómo resolver límites infinitos negativos de manera sencilla y eficaz.

¿Qué son los límites infinitos negativos?

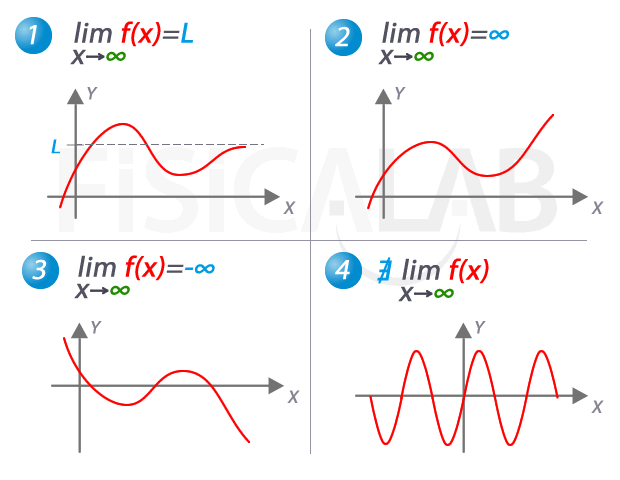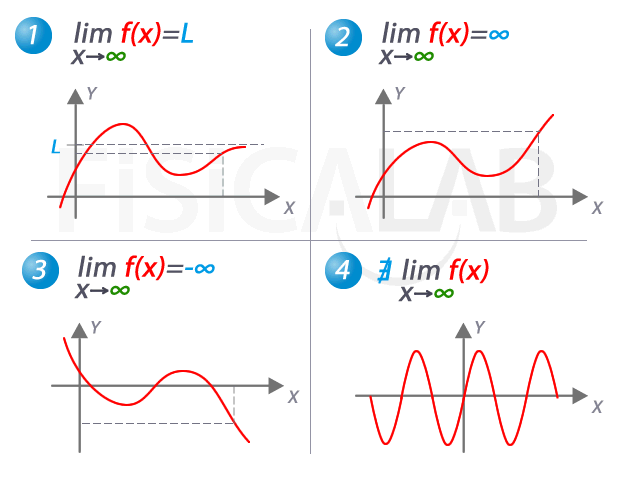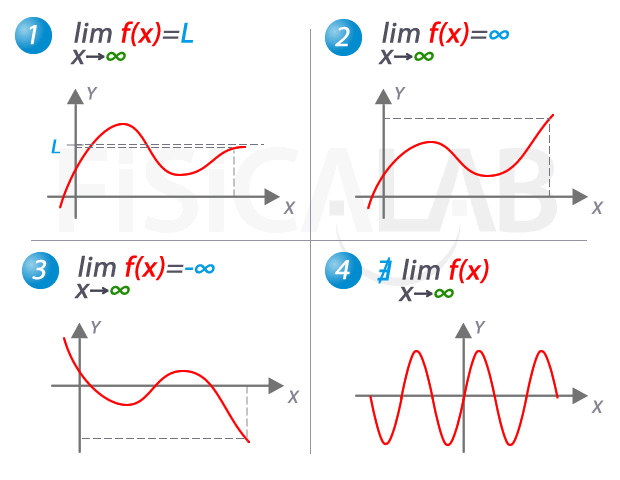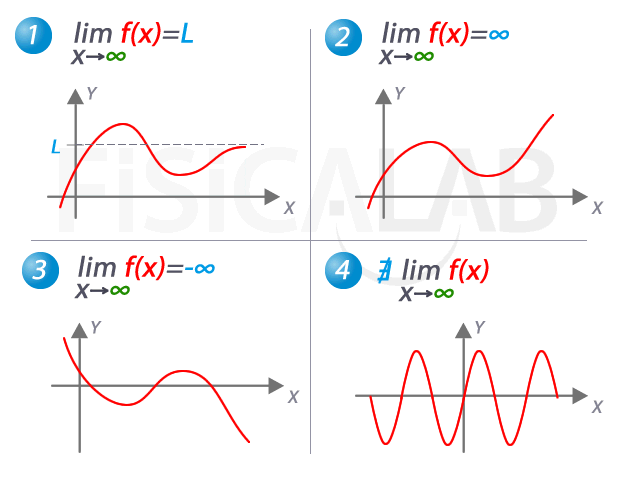
Un límite infinito negativo ocurre cuando la función se acerca a menos infinito (–∞) cuando x se acerca a un cierto valor. En otras palabras, la gráfica de la función se acerca cada vez más a la línea horizontal que representa el eje y a medida que x se acerca a un valor específico. Esto puede ocurrir cuando la función tiene un comportamiento asintótico.

¿Cómo resolver límites infinitos negativos?

Para resolver límites infinitos negativos, existen varias técnicas que puedes utilizar:

Multiplicar por el conjugado

Una de las técnicas más comunes para resolver límites infinitos negativos es multiplicar la función por su conjugado. Esto se hace para eliminar términos radicales o factores cuadráticos que puedan estar en la función. Por ejemplo, si tenemos el límite:

lim x → –∞ (2x + 5) / (x^2 + 1)

Podemos multiplicar el numerador y el denominador por (2x – 5), que es el conjugado de (2x + 5):

lim x → –∞ [(2x + 5) * (2x – 5)] / [(x^2 + 1) * (2x – 5)]

Al expandir el numerador y simplificar, obtenemos:

lim x → –∞ (4x^2 – 25) / (2x^3 – 5x^2 + 2x – 5)

Este límite puede ser resuelto utilizando otras técnicas.

Dividir por la variable de mayor grado

Otra técnica que puedes utilizar para resolver límites infinitos negativos es dividir la función por la variable de mayor grado. Por ejemplo, si tenemos el límite:

lim x → –∞ (3x^3 + 4x^2 – 5x + 2) / (5x^3 – 2x^2 + 3)

Podemos dividir tanto el numerador como el denominador por x^3:

lim x → –∞ (3 + 4/x – 5/x^2 + 2/x^3) / (5 – 2/x + 3/x^3)

Al tomar el límite, podemos ver que los términos con x en el denominador se hacen infinitamente pequeños, por lo que podemos eliminarlos. Así, obtenemos:

lim x → –∞ (3/5)

Usar la regla de L'Hôpital

La regla de L'Hôpital es una técnica que se utiliza cuando se tiene un límite indeterminado. Se aplica cuando tanto el numerador como el denominador tienden a cero o infinito. Es decir, si tenemos el límite:

lim x → –∞ f(x) / g(x)

Y tanto f(x) como g(x) tienden a cero o infinito, podemos derivar tanto el numerador como el denominador y tomar el límite de la derivada. El resultado será el mismo que el límite original.

Conclusión

Los límites infinitos negativos pueden parecer intimidantes, pero con las técnicas adecuadas, pueden ser resueltos fácilmente. Al utilizar la multiplicación por el conjugado, la división por la variable de mayor grado o la regla de L'Hôpital, puedes resolver cualquier límite infinito negativo que se te presente.

Preguntas frecuentes

¿Qué es un límite infinito negativo?

Un límite infinito negativo ocurre cuando la función se acerca a menos infinito (–∞) cuando x se acerca a un cierto valor.

¿Cómo se resuelve un límite infinito negativo?

Para resolver un límite infinito negativo, puedes utilizar técnicas como la multiplicación por el conjugado, la división por la variable de mayor grado o la regla de L'Hôpital.

¿Qué es la regla de L'Hôpital?

La regla de L'Hôpital es una técnica que se utiliza cuando se tiene un límite indeterminado. Se aplica cuando tanto el numerador como el denominador tienden a cero o infinito.

¿Cuál es la técnica más común para resolver límites infinitos negativos?

La técnica más común para resolver límites infinitos negativos es la multiplicación por el conjugado.

¿Por qué es importante saber cómo resolver límites infinitos negativos?

Saber cómo resolver límites infinitos negativos es importante para comprender el comportamiento de las funciones y resolver problemas matemáticos más complejos. Además, es una habilidad clave para estudiantes de matemáticas y ciencias.