Descubre cómo entender la teoría de grafos de forma sencilla

Cuando hablamos de la teoría de grafos, puede sonar como un tema complejo y difícil de entender. Sin embargo, esta rama de las matemáticas aplicadas puede ser más sencilla de lo que parece. En este artículo, te explicaremos de manera clara y concisa qué es la teoría de grafos y cómo puedes entenderla de forma sencilla.

¿Qué es la teoría de grafos?

En general, la teoría de grafos es una rama de las matemáticas que se enfoca en el estudio de las relaciones entre objetos. Un grafo es un conjunto de nodos (también llamados vértices) que están conectados por líneas (también llamadas aristas).

Los grafos se utilizan en diversos campos, desde la informática hasta la biología, para modelar situaciones en las que hay relaciones entre objetos. Por ejemplo, un grafo podría usarse para representar una red de computadoras o una red de transporte público.

¿Cómo se representan los grafos?

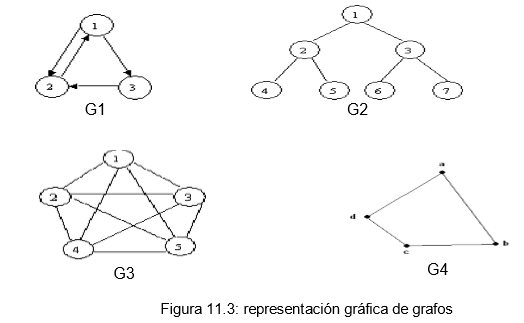
Los grafos se pueden representar de diferentes maneras, pero una de las más comunes es mediante un diagrama en el que los nodos se muestran como puntos y las aristas como líneas que conectan los nodos. Por ejemplo, el siguiente grafo muestra una red de ciudades y las carreteras que las conectan:


También es posible representar los grafos mediante matrices. En una matriz de adyacencia, las filas y columnas representan los nodos, y los elementos de la matriz indican si hay una arista que conecta los nodos correspondientes. Por ejemplo, la matriz de adyacencia para el grafo anterior sería:

```
A B C D
A 0 1 0 1
B 1 0 1 1
C 0 1 0 1
D 1 1 1 0
```

Tipos de grafos

Existen diferentes tipos de grafos, dependiendo de las características que poseen. Algunos de los tipos más comunes son:

• Grafo dirigido: en este tipo de grafo, las aristas tienen una dirección. Por ejemplo, una arista podría ir desde el nodo A hacia el nodo B, pero no en sentido contrario.
• Grafo no dirigido: en este tipo de grafo, las aristas no tienen una dirección, lo que significa que se puede ir de un nodo a otro en ambos sentidos.
• Grafo ponderado: en este tipo de grafo, las aristas tienen un peso o valor asociado. Por ejemplo, en una red de carreteras, el peso podría representar la distancia entre dos ciudades.
• Grafo bipartito: en este tipo de grafo, los nodos se pueden dividir en dos conjuntos disjuntos, de manera que no haya aristas que conecten nodos del mismo conjunto.

Algoritmos de grafos

Una de las aplicaciones más comunes de la teoría de grafos es el desarrollo de algoritmos que permiten resolver problemas relacionados con grafos. Algunos de los algoritmos más comunes son:

• Algoritmo de Dijkstra: este algoritmo se utiliza para encontrar el camino más corto entre dos nodos en un grafo ponderado con aristas no negativas.
• Algoritmo de Kruskal: este algoritmo se utiliza para encontrar el árbol de expansión mínima de un grafo ponderado.
• Algoritmo de Floyd-Warshall: este algoritmo se utiliza para encontrar el camino más corto entre todos los pares de nodos en un grafo ponderado con aristas no negativas.

Conclusión

La teoría de grafos es una rama de las matemáticas que se enfoca en el estudio de las relaciones entre objetos. Los grafos se pueden representar de diferentes maneras y existen diferentes tipos de grafos, dependiendo de sus características. Los algoritmos de grafos se utilizan para resolver problemas relacionados con grafos en diversos campos, desde la informática hasta la biología.

Preguntas frecuentes

¿Qué es un camino en un grafo?

Un camino en un grafo es una secuencia de nodos conectados por aristas. Por ejemplo, en el grafo de la red de ciudades anterior, un camino podría ser "A-B-C".

¿Qué es un ciclo en un grafo?

Un ciclo en un grafo es un camino cerrado que comienza y termina en el mismo nodo. Por ejemplo, en el grafo de la red de ciudades anterior, un ciclo podría ser "B-C-D-B".

¿Qué es un grafo conexo?

Un grafo es conexo si existe un camino entre cualquier par de nodos. En otras palabras, no hay nodos aislados en el grafo.

¿Qué es un grafo completo?

Un grafo es completo si hay una arista que conecta cualquier par de nodos. En otras palabras, no hay nodos aislados en el grafo y cada par de nodos está conectado por una arista.

¿Qué es un grafo acíclico?

Un grafo es acíclico si no tiene ciclos. En otras palabras, no hay un camino cerrado que comience y termine en el mismo nodo.