Descubre cómo encontrar razones trigonométricas en ángulos

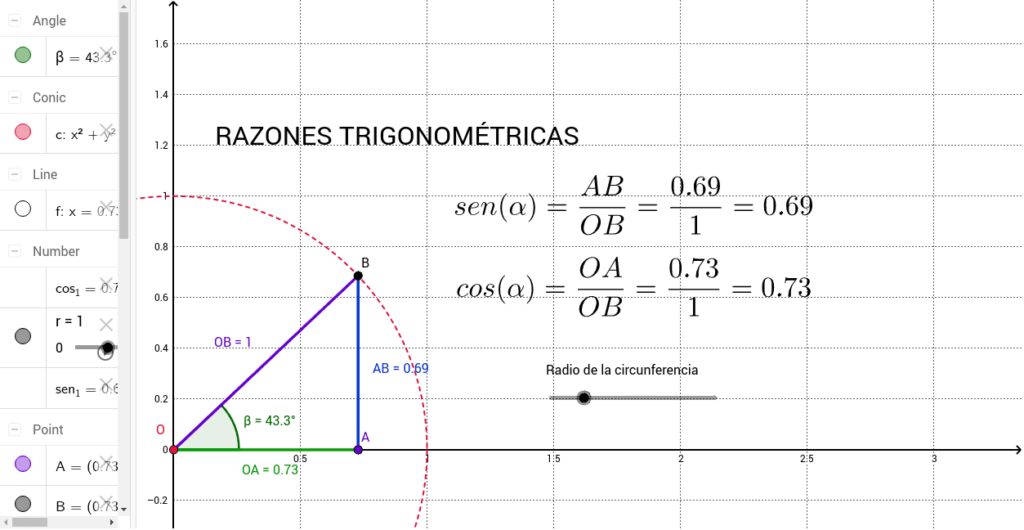
Los ángulos son una parte fundamental de la geometría, la física y las matemáticas en general. Una de las ramas de las matemáticas que se enfoca en el estudio de los ángulos es la trigonometría. En la trigonometría, las razones trigonométricas son las relaciones entre los lados de un triángulo rectángulo y sus ángulos. En este artículo, te enseñaremos cómo encontrar las razones trigonométricas en ángulos.

¿Qué son las razones trigonométricas?

Las razones trigonométricas son las relaciones entre los lados de un triángulo rectángulo y sus ángulos. Estas razones son el seno, el coseno y la tangente. Cada una de estas razones se define como sigue:

- Seno: la razón entre el lado opuesto al ángulo y la hipotenusa.
- Coseno: la razón entre el lado adyacente al ángulo y la hipotenusa.
- Tangente: la razón entre el lado opuesto al ángulo y el lado adyacente al ángulo.

¿Cómo encontrar las razones trigonométricas?

Para encontrar las razones trigonométricas de un ángulo, necesitas un triángulo rectángulo en el cual el ángulo es uno de los ángulos agudos. Luego, puedes utilizar las siguientes fórmulas:

- Seno: seno del ángulo = lado opuesto / hipotenusa
- Coseno: coseno del ángulo = lado adyacente / hipotenusa
- Tangente: tangente del ángulo = lado opuesto / lado adyacente

Ejemplo 1:

Supongamos que tenemos un triángulo rectángulo con un ángulo de 30 grados. La hipotenusa del triángulo mide 10 cm. Para encontrar el seno, el coseno y la tangente del ángulo, podemos utilizar las fórmulas:

- Seno: seno de 30 grados = lado opuesto / hipotenusa. Como el ángulo de 30 grados es opuesto al lado más corto del triángulo, el lado opuesto mide la mitad de la hipotenusa. Por lo tanto, el seno de 30 grados es 1/2.
- Coseno: coseno de 30 grados = lado adyacente / hipotenusa. Como el ángulo de 30 grados es adyacente al lado más largo del triángulo, el lado adyacente mide la mitad de la hipotenusa multiplicado por la raíz cuadrada de 3. Por lo tanto, el coseno de 30 grados es raíz cuadrada de 3 / 2.
- Tangente: tangente de 30 grados = lado opuesto / lado adyacente. Como ya hemos encontrado que el lado opuesto mide la mitad de la hipotenusa y el lado adyacente mide la mitad de la hipotenusa multiplicado por la raíz cuadrada de 3, podemos simplificar la fórmula para obtener la tangente como 1 / raíz cuadrada de 3.

Ejemplo 2:

Supongamos que tenemos un triángulo rectángulo con un ángulo de 45 grados. La hipotenusa del triángulo mide 10 cm. Para encontrar el seno, el coseno y la tangente del ángulo, podemos utilizar las fórmulas:

- Seno: seno de 45 grados = lado opuesto / hipotenusa. Como el ángulo de 45 grados es opuesto al lado más corto del triángulo y este lado es igual al lado adyacente, podemos utilizar el teorema de Pitágoras para encontrar que el lado adyacente mide la hipotenusa dividida por la raíz cuadrada de 2. Por lo tanto, el seno de 45 grados es 1 / raíz cuadrada de 2.
- Coseno: coseno de 45 grados = lado adyacente / hipotenusa. Como ya hemos encontrado que el lado adyacente mide la hipotenusa dividida por la raíz cuadrada de 2, podemos simplificar la fórmula para obtener el coseno como 1 / raíz cuadrada de 2.
- Tangente: tangente de 45 grados = lado opuesto / lado adyacente. Como ya hemos encontrado que el lado adyacente mide la hipotenusa dividida por la raíz cuadrada de 2 y el lado opuesto es igual al lado adyacente, podemos simplificar la fórmula para obtener la tangente como 1.

Conclusión

Las razones trigonométricas son fundamentales para el estudio de la trigonometría y la resolución de problemas en diversas áreas de las matemáticas y la física. Para encontrar las razones trigonométricas de un ángulo, es necesario conocer un triángulo rectángulo en el cual el ángulo es uno de los ángulos agudos. Utilizando las fórmulas adecuadas, podemos encontrar el seno, el coseno y la tangente de un ángulo.

Preguntas frecuentes

1. ¿Es posible encontrar las razones trigonométricas de cualquier ángulo?

No, solamente es posible encontrar las razones trigonométricas de ángulos agudos en triángulos rectángulos.

2. ¿Por qué son importantes las razones trigonométricas?

Las razones trigonométricas son importantes porque nos permiten resolver problemas en diversas áreas de las matemáticas y la física, como la navegación, la ingeniería y la arquitectura.

3. ¿Qué ocurre si el triángulo rectángulo no tiene una hipotenusa?

Todos los triángulos rectángulos tienen una hipotenusa, que es el lado más largo del triángulo y que está opuesto al ángulo recto.

4. ¿Puedo utilizar las razones trigonométricas para encontrar la medida de un ángulo?

Sí, es posible utilizar las razones trigonométricas para encontrar la medida de un ángulo si conocemos dos de las tres razones trigonométricas de ese ángulo.

5. ¿Qué es el teorema de Pitágoras?

El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. Esta fórmula es fundamental para el cálculo de las razones trigonométricas.