Descubre cómo calcular las razones trigonométricas de un ángulo agudo
En la geometría y la trigonometría, los ángulos son una medida importante para describir la relación entre distintos objetos o puntos en el espacio. Los ángulos pueden ser agudos, obtusos o rectos, y cada uno de ellos tiene propiedades específicas. En este artículo, te mostraremos cómo calcular las razones trigonométricas de un ángulo agudo, utilizando diferentes herramientas y técnicas.
¿Qué son las razones trigonométricas?
Las razones trigonométricas son un conjunto de funciones matemáticas que se utilizan para describir la relación entre los lados y los ángulos de un triángulo rectángulo. En un triángulo rectángulo, el ángulo más agudo es siempre el que se encuentra opuesto al lado más corto, también conocido como la hipotenusa. Las tres razones trigonométricas principales son el seno, el coseno y la tangente, y se suelen representar por las letras "sin", "cos" y "tan", respectivamente.
Cómo calcular el seno, el coseno y la tangente de un ángulo agudo
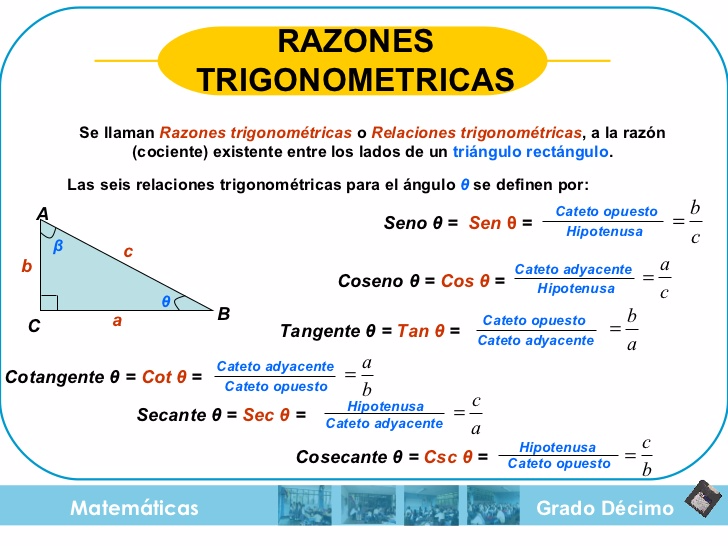
Para calcular las razones trigonométricas de un ángulo agudo, primero debemos conocer la medida de los lados del triángulo rectángulo que lo contiene. A continuación, se muestran las fórmulas para calcular el seno, el coseno y la tangente de un ángulo agudo, utilizando las medidas de los lados del triángulo:
- El seno de un ángulo agudo se calcula dividiendo el lado opuesto al ángulo entre la hipotenusa: sen = (lado opuesto) / (hipotenusa).
- El coseno de un ángulo agudo se calcula dividiendo el lado adyacente al ángulo entre la hipotenusa: cos = (lado adyacente) / (hipotenusa).
- La tangente de un ángulo agudo se calcula dividiendo el lado opuesto al ángulo entre el lado adyacente al ángulo: tan = (lado opuesto) / (lado adyacente).
Ejemplo de cálculo de razones trigonométricas
Supongamos que tenemos un triángulo rectángulo con un ángulo agudo de 30 grados, y que conocemos la medida del lado adyacente al ángulo, que es de 2 unidades. Para calcular las razones trigonométricas de este ángulo, podemos utilizar las siguientes fórmulas:
- El seno de 30 grados es igual a (lado opuesto) / (hipotenusa). Como no conocemos la medida del lado opuesto, podemos utilizar el teorema de Pitágoras para calcular la hipotenusa: hipotenusa = sqrt((lado adyacente)^2 + (lado opuesto)^2). En este caso, como conocemos la medida del lado adyacente, podemos despejar la medida del lado opuesto: lado opuesto = sqrt(3) * lado adyacente. Por lo tanto, el seno de 30 grados es igual a sqrt(3) / 2.
- El coseno de 30 grados es igual a (lado adyacente) / (hipotenusa). Utilizando la hipotenusa que acabamos de calcular, el coseno de 30 grados es igual a 1/2.
- La tangente de 30 grados es igual a (lado opuesto) / (lado adyacente). Utilizando la medida del lado opuesto que calculamos anteriormente, la tangente de 30 grados es igual a sqrt(3).
Tabla de razones trigonométricas
En la siguiente tabla se muestran las razones trigonométricas de los ángulos más comunes, expresadas en fracciones y en decimales:
| Ángulo | Seno | Coseno | Tangente |
|---|---|---|---|
| 0° | 0/1 = 0 | 1/1 = 1 | 0/1 = 0 |
| 30° | 1/2 = 0.5 | sqrt(3)/2 = 0.866 | sqrt(3)/3 = 0.577 |
| 45° | sqrt(2)/2 = 0.707 | sqrt(2)/2 = 0.707 | 1/1 = 1 |
| 60° | sqrt(3)/2 = 0.866 | 1/2 = 0.5 | sqrt(3) = 1.732 |
| 90° | 1/1 = 1 | 0/1 = 0 | no definido |
Conclusión
Calcular las razones trigonométricas de un ángulo agudo es una habilidad muy útil en la matemática, la física y otras disciplinas. Al conocer estas razones, podemos describir la relación entre los lados y los ángulos de un triángulo rectángulo de manera precisa y sencilla, lo que nos permite resolver problemas y hacer cálculos de manera más eficiente. Recuerda que para calcular las razones trigonométricas de un ángulo agudo, debes conocer la medida de al menos uno de los lados del triángulo rectángulo que lo contiene, y aplicar las fórmulas adecuadas.
Preguntas frecuentes
1. ¿Qué es un triángulo rectángulo?
Un triángulo rectángulo es un tipo de triángulo que tiene un ángulo recto, es decir, un ángulo de 90 grados. En un triángulo rectángulo, los otros dos ángulos son siempre agudos, es decir, menores a 90 grados. Este tipo de triángulo es muy importante en la geometría y la trigonometría, ya que permite describir relaciones entre los lados y los ángulos de manera sencilla y precisa.
2. ¿Qué es la hipotenusa de un triángulo rectángulo?
La hip
Deja una respuesta