Conectores lógicos: la clave de la lógica matemática

La lógica matemática es esencial en el mundo de las matemáticas, y una de las herramientas más importantes en este campo son los conectores lógicos. Los conectores lógicos son palabras o frases que se utilizan para conectar proposiciones, lo que permite construir argumentos lógicos. En este artículo, discutiremos los diferentes tipos de conectores lógicos y cómo se utilizan en la lógica matemática.

¿Qué son los conectores lógicos?

Los conectores lógicos son palabras o frases que se utilizan para conectar proposiciones. En la lógica matemática, las proposiciones son declaraciones que pueden ser verdaderas o falsas. Por ejemplo, "2 + 2 = 4" es una proposición verdadera, mientras que "2 + 2 = 5" es una proposición falsa.

Los conectores lógicos se utilizan para conectar dos o más proposiciones, lo que permite construir argumentos lógicos. Por ejemplo, "Si A es mayor que B y B es mayor que C, entonces A es mayor que C" es un argumento lógico que utiliza el conector lógico "y" para conectar las dos proposiciones.

Tipos de conectores lógicos

Existen varios tipos de conectores lógicos, cada uno con su propia función en la lógica matemática. A continuación, se presentan algunos de los conectores lógicos más comunes:

Conjunción

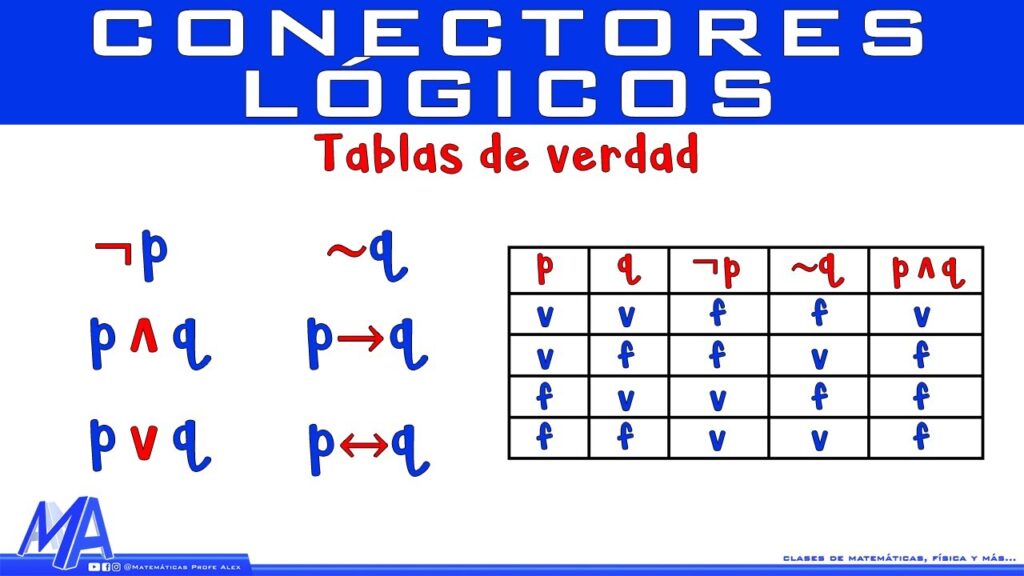
La conjunción se utiliza para conectar dos proposiciones y se representa por el símbolo "∧". Por ejemplo, "A es mayor que B ∧ B es mayor que C" es una proposición conjunta que indica que ambas proposiciones son verdaderas.

Disyunción

La disyunción se utiliza para conectar dos proposiciones y se representa por el símbolo "∨". Por ejemplo, "A es mayor que B ∨ B es mayor que C" es una proposición disyuntiva que indica que al menos una de las proposiciones es verdadera.

Negación

La negación se utiliza para negar una proposición y se representa por el símbolo "¬". Por ejemplo, "No es cierto que A es mayor que B" es una proposición negada que indica que la proposición opuesta es verdadera.

Implicación

La implicación se utiliza para indicar una relación de causa y efecto entre dos proposiciones y se representa por el símbolo "→". Por ejemplo, "Si A es mayor que B, entonces A es mayor que C" es una proposición implicada que indica que la primera proposición es la causa de la segunda proposición.

Equivalencia

La equivalencia se utiliza para indicar que dos proposiciones tienen el mismo valor de verdad y se representa por el símbolo "↔". Por ejemplo, "A es mayor que B ↔ B es menor que A" es una proposición equivalente que indica que ambas proposiciones tienen el mismo valor de verdad.

Cómo utilizar los conectores lógicos en la lógica matemática

Los conectores lógicos son esenciales en la lógica matemática, ya que permiten construir argumentos lógicos. Para utilizar los conectores lógicos en la lógica matemática, se deben seguir los siguientes pasos:

Paso 1: Identificar las proposiciones

El primer paso para utilizar los conectores lógicos en la lógica matemática es identificar las proposiciones que se van a utilizar. Las proposiciones pueden ser simples o compuestas y deben ser verdaderas o falsas.

Paso 2: Escoger el conector lógico adecuado

El segundo paso es escoger el conector lógico adecuado para conectar las proposiciones. El conector lógico adecuado dependerá del tipo de relación que se quiera establecer entre las proposiciones.

Paso 3: Escribir la proposición compuesta

El tercer paso es escribir la proposición compuesta utilizando el conector lógico adecuado. La proposición compuesta debe ser clara y fácil de entender.

Paso 4: Evaluar la proposición compuesta

El cuarto y último paso es evaluar la proposición compuesta para determinar si es verdadera o falsa. Para evaluar la proposición compuesta, se deben evaluar cada una de las proposiciones individuales y luego aplicar el conector lógico adecuado.

Conclusiones

Los conectores lógicos son esenciales en la lógica matemática, ya que permiten construir argumentos lógicos. Existen varios tipos de conectores lógicos, cada uno con su propia función en la lógica matemática. Para utilizar los conectores lógicos en la lógica matemática, se deben seguir los pasos de identificar las proposiciones, escoger el conector lógico adecuado, escribir la proposición compuesta y evaluar la proposición compuesta.

Preguntas frecuentes

1. ¿Qué son los conectores lógicos?

Los conectores lógicos son palabras o frases que se utilizan para conectar proposiciones, lo que permite construir argumentos lógicos.

2. ¿Cuáles son los tipos de conectores lógicos?

Los tipos de conectores lógicos incluyen la conjunción, la disyunción, la negación, la implicación y la equivalencia.

3. ¿Cómo se utilizan los conectores lógicos en la lógica matemática?

Para utilizar los conectores lógicos en la lógica matemática, se deben seguir los pasos de identificar las proposiciones, escoger el conector lógico adecuado, escribir la proposición compuesta y evaluar la proposición compuesta.

4. ¿Por qué son importantes los conectores lógicos en la lógica matemática?

Los conectores lógicos son importantes en la lógica matemática porque permiten construir argumentos lógicos y establecer relaciones entre proposiciones.

5. ¿Cómo puedo mejorar mi comprensión de los conectores lógicos?

Para mejorar la comprensión de los conectores lógicos, se recomienda practicar la identificación y uso de los diferentes tipos de conectores lógicos en diferentes ejemplos y situaciones. También se pueden utilizar recursos en línea y libros de texto para aprender más sobre los conectores lógicos.