Conectores lógicos en matemáticas: guía completa para entenderlos
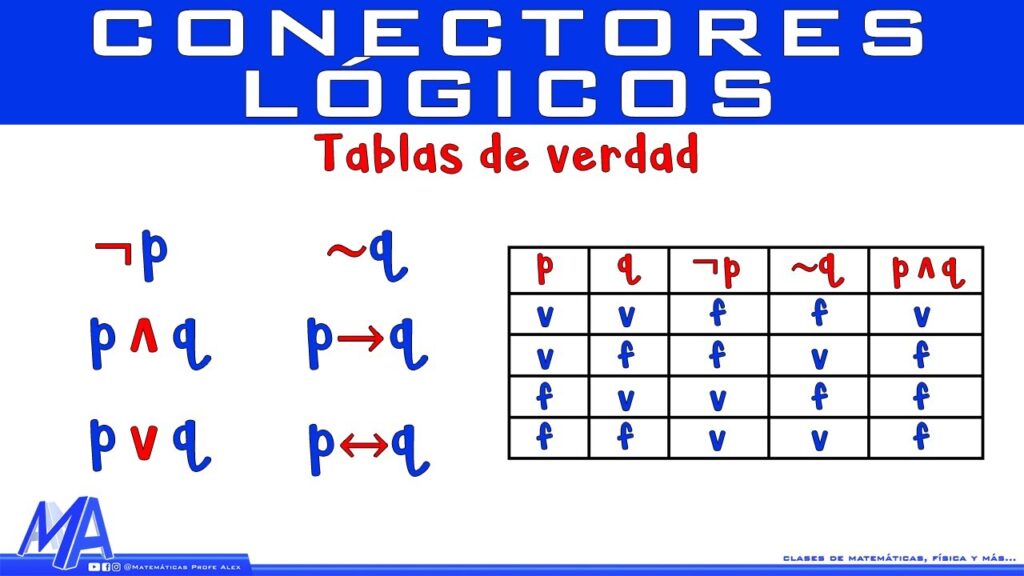
Si has estudiado matemáticas, es probable que en algún momento hayas escuchado hablar de los conectores lógicos. Estos son términos que se utilizan para unir proposiciones y expresar relaciones lógicas entre ellas. En este artículo, te explicaremos todo lo que necesitas saber sobre los conectores lógicos en matemáticas.
¿Qué son los conectores lógicos?
Los conectores lógicos son palabras o símbolos que se utilizan para unir proposiciones y expresar relaciones lógicas entre ellas. En matemáticas, se utilizan principalmente tres conectores lógicos: "y", "o" y "si...entonces".
Conector "y"
El conector "y" se utiliza para unir dos proposiciones que son verdaderas al mismo tiempo. Por ejemplo, si decimos "Juan es alto y María es inteligente", estamos diciendo que ambas proposiciones son verdaderas al mismo tiempo.
Conector "o"
El conector "o" se utiliza para unir dos proposiciones, indicando que al menos una de ellas es verdadera. Por ejemplo, si decimos "Juan es alto o María es inteligente", estamos diciendo que, aunque no sabemos si ambas proposiciones son verdaderas, al menos una de ellas lo es.
Conector "si...entonces"
El conector "si...entonces" se utiliza para expresar una relación de implicación entre dos proposiciones. Por ejemplo, si decimos "si llueve, entonces me quedo en casa", estamos diciendo que, si la primera proposición es verdadera (llueve), entonces la segunda también debe serlo (me quedo en casa).
Usos de los conectores lógicos en matemáticas
Los conectores lógicos son fundamentales en matemáticas, ya que se utilizan para expresar relaciones lógicas entre proposiciones. Algunos de los usos más comunes son:
- En la lógica proposicional, se utilizan para construir fórmulas lógicas que puedan ser evaluadas como verdaderas o falsas.
- En la geometría, se utilizan para expresar relaciones entre figuras geométricas.
- En el cálculo, se utilizan para expresar relaciones entre funciones y sus derivadas.
Ejemplos de conectores lógicos en matemáticas
A continuación, te presentamos algunos ejemplos de cómo se utilizan los conectores lógicos en matemáticas:
- En lógica proposicional: "p y q", "p o q", "si p entonces q".
- En geometría: "el segmento AB es paralelo al segmento CD y el segmento CD es perpendicular al segmento EF".
- En cálculo: "si f(x) es continua en [a,b], entonces f(x) es integrable en [a,b]".
Conectores lógicos y negación
Además de los conectores lógicos, es importante mencionar la negación. La negación se utiliza para expresar que una proposición es falsa. Por ejemplo, si decimos "no llueve", estamos negando la proposición "llueve".
En matemáticas, la negación se representa con el símbolo "~". Por ejemplo, si decimos "~p", estamos negando la proposición "p". La negación también se puede utilizar en combinación con los conectores lógicos para expresar proposiciones más complejas.
Conclusiones
Los conectores lógicos son fundamentales en matemáticas, ya que se utilizan para expresar relaciones lógicas entre proposiciones. Los tres conectores lógicos principales en matemáticas son "y", "o" y "si...entonces". Además, es importante mencionar la negación, que se utiliza para expresar que una proposición es falsa.
Esperamos que esta guía te haya sido útil para entender los conectores lógicos en matemáticas. Si tienes alguna duda o comentario, no dudes en dejarlo en la sección de comentarios.
Preguntas frecuentes
1. ¿Qué son los conectores lógicos en matemáticas?
Los conectores lógicos son palabras o símbolos que se utilizan para unir proposiciones y expresar relaciones lógicas entre ellas.
2. ¿Cuáles son los conectores lógicos principales en matemáticas?
Los tres conectores lógicos principales en matemáticas son "y", "o" y "si...entonces".
3. ¿Para qué se utilizan los conectores lógicos en matemáticas?
Los conectores lógicos se utilizan para expresar relaciones lógicas entre proposiciones. En matemáticas, se utilizan principalmente en la lógica proposicional, la geometría y el cálculo.
4. ¿Qué es la negación en matemáticas?
La negación se utiliza para expresar que una proposición es falsa. En matemáticas, se representa con el símbolo "~".
5. ¿Cómo se utilizan los conectores lógicos en combinación con la negación?
La negación se puede utilizar en combinación con los conectores lógicos para expresar proposiciones más complejas. Por ejemplo, "~p o q" significa "no p o q".
Deja una respuesta