Conecta tus conocimientos con la lógica: Aprende Álgebra Booleana

¿Qué es el Álgebra Booleana?

El Álgebra Booleana es una rama de la matemática que se enfoca en el estudio de las operaciones lógicas y algebraicas. Esta rama de la matemática es muy importante en el mundo de la tecnología y la informática, ya que se utiliza para la programación de computadoras y la creación de circuitos lógicos.

En términos simples, el Álgebra Booleana se trata de una herramienta matemática que nos permite trabajar con valores lógicos (verdadero o falso) y operaciones lógicas (AND, OR, NOT) para resolver problemas o crear sistemas complejos.

¿Por qué es importante aprender Álgebra Booleana?

El Álgebra Booleana es una herramienta esencial para los estudiantes de ciencias de la computación, electrónica y tecnología de la información. A través de la comprensión de esta rama de la matemática, los estudiantes pueden desarrollar habilidades para crear sistemas de hardware y software más eficientes y efectivos.

Además, el Álgebra Booleana puede ser utilizada en la vida cotidiana, para resolver problemas lógicos y tomar decisiones informadas. Por lo tanto, aprender Álgebra Booleana puede ser beneficioso para cualquier persona que desee mejorar su habilidad para resolver problemas lógicos y tomar decisiones informadas.

Conceptos básicos del Álgebra Booleana

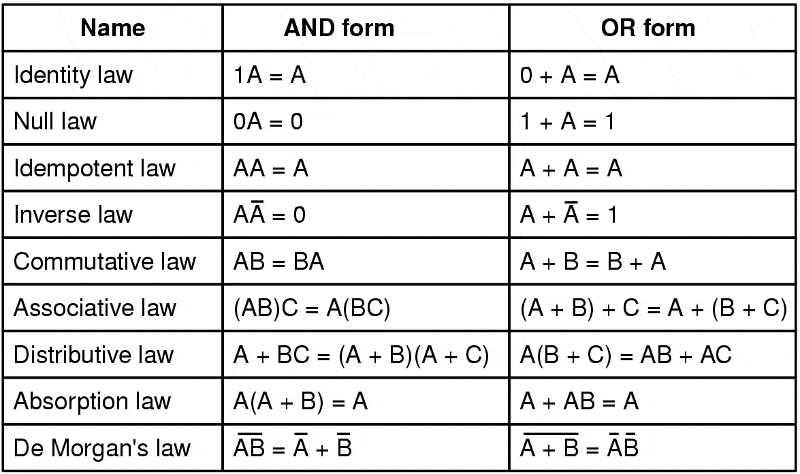
Antes de profundizar en el Álgebra Booleana, es importante entender algunos conceptos básicos. En el Álgebra Booleana, los valores lógicos se representan mediante dos valores: verdadero (1) o falso (0). Las operaciones lógicas básicas son AND, OR y NOT.

La operación AND se utiliza para evaluar si dos valores lógicos son verdaderos. Si ambos valores son verdaderos, el resultado será verdadero. De lo contrario, el resultado será falso.

La operación OR se utiliza para evaluar si al menos uno de los valores es verdadero. Si uno o ambos valores son verdaderos, el resultado será verdadero. Solo si ambos valores son falsos, el resultado será falso.

La operación NOT se utiliza para negar el valor de una expresión. Si el valor original es verdadero, el resultado será falso. Si el valor original es falso, el resultado será verdadero.

Aplicaciones del Álgebra Booleana

El Álgebra Booleana tiene muchas aplicaciones en el mundo de la tecnología y la informática. Por ejemplo, se utiliza para la creación de circuitos lógicos, el diseño de sistemas de control, y la programación de computadoras.

Además, el Álgebra Booleana se utiliza en la criptografía, la seguridad informática y la inteligencia artificial. En la criptografía, se utiliza para el cifrado y descifrado de mensajes. En la seguridad informática, se utiliza para la autenticación de usuarios y el control de acceso a sistemas. En la inteligencia artificial, se utiliza para la creación de sistemas de razonamiento lógico.

Consejos para aprender Álgebra Booleana

Aprender Álgebra Booleana puede parecer intimidante al principio, pero con la práctica y la perseverancia, es posible dominar esta rama de la matemática. Aquí hay algunos consejos para ayudarte a aprender Álgebra Booleana:

1. Comprende los conceptos básicos: Antes de profundizar en el Álgebra Booleana, es importante tener una comprensión sólida de los conceptos básicos.
2. Practica con ejercicios: La mejor manera de aprender Álgebra Booleana es practicando con ejercicios.
3. Utiliza recursos en línea: Hay muchos recursos en línea disponibles para ayudarte a aprender Álgebra Booleana.
4. Busca ayuda cuando sea necesario: Si tienes dificultades para entender un concepto, no dudes en buscar ayuda.

Conclusión

El Álgebra Booleana es una herramienta matemática esencial para los estudiantes de ciencias de la computación, electrónica y tecnología de la información. A través de la comprensión de esta rama de la matemática, los estudiantes pueden desarrollar habilidades para crear sistemas de hardware y software más eficientes y efectivos. Además, el Álgebra Booleana puede ser utilizada en la vida cotidiana, para resolver problemas lógicos y tomar decisiones informadas.

Preguntas frecuentes

1. ¿Cuál es la diferencia entre el Álgebra Booleana y la lógica proposicional?

El Álgebra Booleana y la lógica proposicional son esencialmente lo mismo. La diferencia radica en la notación y el enfoque. El Álgebra Booleana utiliza la notación algebraica y se enfoca en la manipulación de expresiones booleanas. La lógica proposicional utiliza la notación simbólica y se enfoca en la evaluación de proposiciones.

2. ¿Es difícil aprender Álgebra Booleana?

Aprender Álgebra Booleana puede ser desafiante al principio, pero con la práctica y la perseverancia, es posible dominar esta rama de la matemática.

3. ¿Dónde se utiliza el Álgebra Booleana en la vida cotidiana?

El Álgebra Booleana se utiliza en la vida cotidiana para resolver problemas lógicos y tomar decisiones informadas.

4. ¿Es necesario aprender Álgebra Booleana para programar una computadora?

Sí, el Álgebra Booleana es esencial para la programación de computadoras.

5. ¿Dónde puedo encontrar recursos en línea para aprender Álgebra Booleana?

Hay muchos recursos en línea disponibles para aprender Álgebra Booleana, incluyendo tutoriales, ejercicios y videos educativos. Algunos sitios recomendados incluyen Khan Academy, Coursera y Udemy.