Cálculo de proposiciones: lógica matemática en acción
La lógica matemática es una rama de las matemáticas que estudia la estructura y el razonamiento formal. En particular, la lógica matemática se ocupa de la manipulación y el cálculo de proposiciones. Las proposiciones son afirmaciones que pueden ser verdaderas o falsas. Por ejemplo, "El cielo es azul" es una proposición que puede ser verdadera o falsa dependiendo de la hora del día y las condiciones climáticas.
El cálculo de proposiciones es una herramienta fundamental en la lógica matemática. Permite analizar y manipular proposiciones para llegar a conclusiones lógicas. El cálculo de proposiciones se basa en la manipulación de conectivas lógicas, que son operadores que relacionan proposiciones. Las principales conectivas lógicas son la negación, la conjunción, la disyunción, la implicación y la equivalencia.
La negación es una conectiva lógica que invierte el valor de verdad de una proposición. Si la proposición es verdadera, su negación es falsa y viceversa. La negación se representa por el símbolo "~". Por ejemplo, si P es la proposición "El cielo es azul", entonces ~P es la proposición "El cielo no es azul".
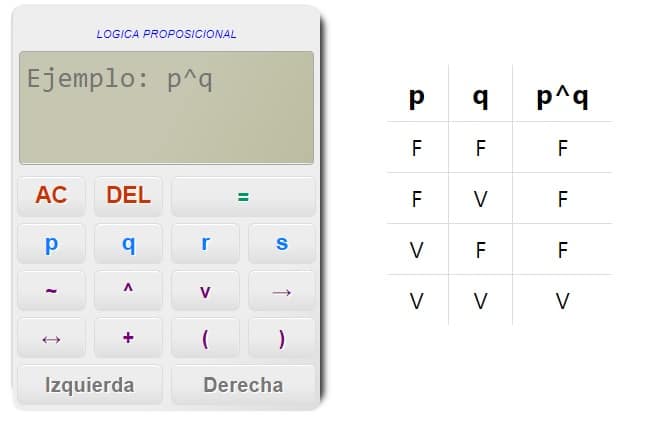
La conjunción es una conectiva lógica que relaciona dos proposiciones y es verdadera si ambas proposiciones son verdaderas. La conjunción se representa por el símbolo "∧". Por ejemplo, si P es la proposición "El cielo es azul" y Q es la proposición "El sol está brillando", entonces P ∧ Q es la proposición "El cielo es azul y el sol está brillando".
La disyunción es una conectiva lógica que relaciona dos proposiciones y es verdadera si al menos una de las proposiciones es verdadera. La disyunción se representa por el símbolo "∨". Por ejemplo, si P es la proposición "El cielo es azul" y Q es la proposición "Está lloviendo", entonces P ∨ Q es la proposición "El cielo es azul o está lloviendo".
La implicación es una conectiva lógica que relaciona dos proposiciones y es falsa si la primera proposición es verdadera y la segunda proposición es falsa. La implicación se representa por el símbolo "→". Por ejemplo, si P es la proposición "El cielo es azul" y Q es la proposición "Está lloviendo", entonces P → Q es la proposición "Si el cielo es azul, entonces no está lloviendo".
La equivalencia es una conectiva lógica que relaciona dos proposiciones y es verdadera si ambas proposiciones tienen el mismo valor de verdad. La equivalencia se representa por el símbolo "↔". Por ejemplo, si P es la proposición "El cielo es azul" y Q es la proposición "El mar es azul", entonces P ↔ Q es la proposición "El cielo es azul si y solo si el mar es azul".
El cálculo de proposiciones se utiliza en muchas áreas de las matemáticas y la informática. Por ejemplo, en la teoría de la computación se utiliza para analizar la complejidad de los algoritmos y en la inteligencia artificial se utiliza para la construcción de sistemas expertos.
El cálculo de proposiciones es una herramienta fundamental en la lógica matemática que permite analizar y manipular proposiciones para llegar a conclusiones lógicas. Las principales conectivas lógicas son la negación, la conjunción, la disyunción, la implicación y la equivalencia. El cálculo de proposiciones se utiliza en muchas áreas de las matemáticas y la informática.
Preguntas frecuentes:
1. ¿Qué es una proposición en lógica matemática?
Una proposición en lógica matemática es una afirmación que puede ser verdadera o falsa.
2. ¿Qué son las conectivas lógicas?
Las conectivas lógicas son operadores que relacionan proposiciones, como la negación, la conjunción, la disyunción, la implicación y la equivalencia.
3. ¿Para qué se utiliza el cálculo de proposiciones?
El cálculo de proposiciones se utiliza para analizar y manipular proposiciones para llegar a conclusiones lógicas, y se aplica en áreas como la teoría de la computación y la inteligencia artificial.
4. ¿Cómo se representa la negación en el cálculo de proposiciones?
La negación se representa por el símbolo "~".
5. ¿Qué es la equivalencia en el cálculo de proposiciones?
La equivalencia es una conectiva lógica que relaciona dos proposiciones y es verdadera si ambas proposiciones tienen el mismo valor de verdad. Se representa por el símbolo "↔".
Deja una respuesta