Calculadora científica: domina las razones trigonométricas
Las razones trigonométricas son una parte fundamental de las matemáticas y son ampliamente utilizadas en campos como la física, la ingeniería y la geometría. Para poder dominar las razones trigonométricas, es necesario tener una buena comprensión de los conceptos básicos de la trigonometría, así como una calculadora científica que pueda realizar los cálculos necesarios de manera rápida y precisa. En este artículo, exploraremos las razones trigonométricas y cómo puedes utilizar tu calculadora científica para dominarlas.
Conceptos básicos de la trigonometría
Antes de poder utilizar tu calculadora científica para dominar las razones trigonométricas, es importante entender los conceptos básicos de la trigonometría. La trigonometría es el estudio de las relaciones entre los ángulos y los lados de un triángulo. En un triángulo rectángulo, el lado más largo se llama hipotenusa y los otros dos lados se llaman catetos. Los ángulos se miden en grados o en radianes.
Las tres razones trigonométricas principales son el seno, el coseno y la tangente. El seno de un ángulo se define como la longitud del cateto opuesto dividido por la longitud de la hipotenusa. El coseno de un ángulo se define como la longitud del cateto adyacente dividido por la longitud de la hipotenusa. La tangente de un ángulo se define como la longitud del cateto opuesto dividido por la longitud del cateto adyacente.
Usando una calculadora científica para dominar las razones trigonométricas
Una calculadora científica es una herramienta esencial para dominar las razones trigonométricas. Una buena calculadora científica debe tener funciones trigonométricas incorporadas, como el seno, coseno y tangente. Para utilizar estas funciones, primero debes asegurarte de que tu calculadora esté configurada en el modo de ángulo correcto. La mayoría de las calculadoras científicas tienen una opción para cambiar entre grados y radianes.
Una vez que tienes tu calculadora en el modo de ángulo correcto, puedes comenzar a utilizar las funciones trigonométricas. Para encontrar el seno de un ángulo, debes ingresar el ángulo y luego presionar el botón "sin" en tu calculadora. Lo mismo ocurre con el coseno y la tangente. Si deseas encontrar la tangente de un ángulo, simplemente ingresa el ángulo y luego presiona el botón "tan" en tu calculadora.
Ejemplos de uso de la calculadora científica para las razones trigonométricas
Veamos algunos ejemplos de cómo puedes utilizar tu calculadora científica para dominar las razones trigonométricas.
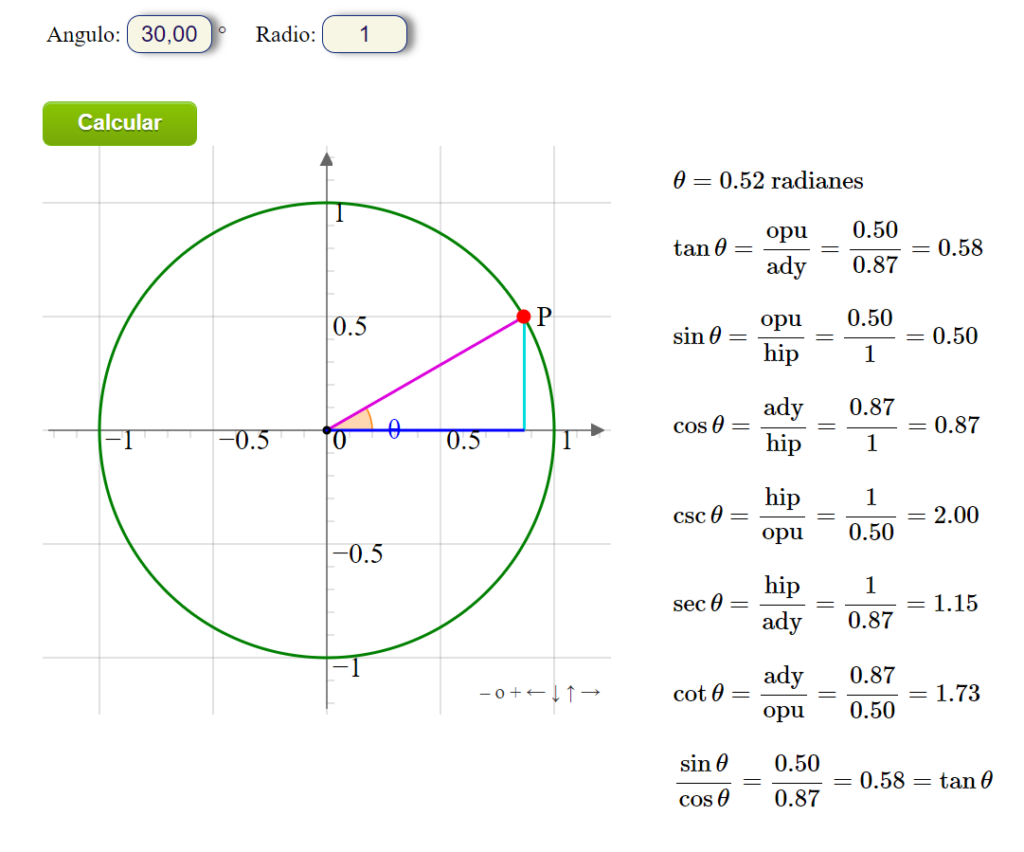
Ejemplo 1: Encuentra el seno, coseno y tangente del ángulo de 30 grados.
Para encontrar el seno de 30 grados, ingresa "30" en tu calculadora y presiona el botón "sin". El resultado será aproximadamente 0.5. Para encontrar el coseno de 30 grados, ingresa "30" en tu calculadora y presiona el botón "cos". El resultado será aproximadamente 0.87. Para encontrar la tangente de 30 grados, ingresa "30" en tu calculadora y presiona el botón "tan". El resultado será aproximadamente 0.58.
Ejemplo 2: Encuentra el ángulo cuyo seno es 0.5.
Para encontrar el ángulo cuyo seno es 0.5, debes utilizar la función inversa del seno, que se denota como "sin-1". Ingresa "0.5" en tu calculadora y presiona el botón "sin-1". El resultado será aproximadamente 30 grados.
Conclusión
Las razones trigonométricas son una parte fundamental de las matemáticas y son ampliamente utilizadas en muchos campos. Para dominar las razones trigonométricas, es importante tener una buena comprensión de los conceptos básicos de la trigonometría y una calculadora científica que pueda realizar los cálculos necesarios de manera rápida y precisa. Con una calculadora científica adecuada y un conocimiento sólido de la trigonometría, puedes dominar las razones trigonométricas y aplicarlas en tus estudios o trabajo.
Preguntas frecuentes
1. ¿Puedo utilizar una calculadora regular para las razones trigonométricas?
No se recomienda el uso de una calculadora regular para las razones trigonométricas. Las calculadoras regulares no tienen funciones trigonométricas incorporadas, por lo que no podrás realizar los cálculos necesarios de manera precisa.
2. ¿Qué debo hacer si mi calculadora no tiene una función inversa?
Si tu calculadora no tiene una función inversa, puedes utilizar la fórmula inversa correspondiente para encontrar el ángulo. Por ejemplo, para encontrar el ángulo cuyo coseno es 0.5, debes utilizar la fórmula inversa del coseno, que se denota como "cos-1".
3. ¿Qué es el teorema de Pitágoras?
El teorema de Pitágoras es un teorema fundamental en la trigonometría que establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos. Es decir, a² + b² = c², donde a y b son los catetos y c es la hipotenusa.
4. ¿Qué es un triángulo isósceles?
Un triángulo isósceles es un triángulo que tiene dos lados de igual longitud y un ángulo opuesto a estos lados de igual medida.
5. ¿Qué es un triángulo equilátero?
Un triángulo equilátero es un triángulo que tiene todos sus lados de igual longitud y todos sus ángulos de igual medida (60 grados).
Deja una respuesta