Axioma de Transitividad: Clave para la Lógica y Matemáticas
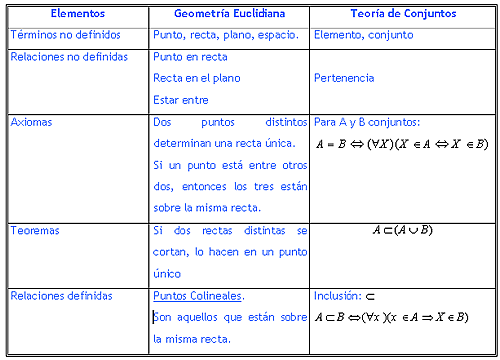
El axioma de transitividad es uno de los conceptos fundamentales en la lógica y las matemáticas. Este axioma establece que si un elemento A está relacionado con un elemento B y este último está relacionado con un elemento C, entonces A también está relacionado con C. En otras palabras, si A es mayor que B y B es mayor que C, entonces A es mayor que C.
Este axioma es esencial para la comprensión y el razonamiento matemático, ya que permite establecer relaciones entre diferentes objetos y establecer órdenes y jerarquías. Además, el axioma de transitividad es uno de los principios básicos de la teoría de conjuntos y la teoría de relaciones.
A continuación, se presentarán algunos ejemplos y aplicaciones del axioma de transitividad.
Aplicaciones del axioma de transitividad en la matemática
Comparación de números
El axioma de transitividad es fundamental para la comparación de números. Si se tiene que A es mayor que B y B es mayor que C, entonces se puede concluir que A es mayor que C. Por ejemplo, si se tiene que 5 es mayor que 3 y 3 es mayor que 1, entonces se puede concluir que 5 es mayor que 1.
Ordenamiento de conjuntos
El axioma de transitividad también es esencial para el ordenamiento de conjuntos. Si se tienen elementos A, B y C, y se establecen relaciones entre ellos, entonces se puede establecer un orden. Por ejemplo, si se tiene un conjunto de palabras {manzana, banana, naranja}, se puede establecer un orden basado en el número de letras de cada palabra. Si se establece la relación "tener más letras que", entonces se puede concluir que "naranja" es mayor que "manzana" y "banana", y que "manzana" es mayor que "banana".
Aplicaciones del axioma de transitividad en la lógica
Razonamiento deductivo
El axioma de transitividad es esencial para el razonamiento deductivo. Si se tienen dos premisas que establecen una relación entre dos elementos, y se puede establecer una tercera premisa que establece una relación entre uno de los elementos de las dos premisas, entonces se puede concluir que hay una relación entre los otros dos elementos. Por ejemplo, si se tiene que "todos los gatos son animales" y "todos los animales tienen cuatro patas", entonces se puede concluir que "todos los gatos tienen cuatro patas".
Teoría de conjuntos
El axioma de transitividad también es esencial para la teoría de conjuntos. Si se tienen dos conjuntos A y B, y se establece una relación entre ellos, entonces se puede establecer una relación entre los elementos de los conjuntos. Por ejemplo, si se tiene que A es un subconjunto de B y B es un subconjunto de C, entonces se puede concluir que A es un subconjunto de C.
Conclusión
El axioma de transitividad es un concepto fundamental en la lógica y las matemáticas. Este axioma permite establecer relaciones entre diferentes objetos y establecer órdenes y jerarquías. Además, es esencial para el razonamiento deductivo, la teoría de conjuntos y la comparación de números.
Preguntas frecuentes
¿Qué es un axioma?
Un axioma es una proposición que se acepta como verdadera sin necesidad de demostración.
¿Por qué es importante el axioma de transitividad?
El axioma de transitividad es importante porque permite establecer relaciones entre diferentes objetos y establecer órdenes y jerarquías. Además, es esencial para el razonamiento deductivo, la teoría de conjuntos y la comparación de números.
¿Cómo se usa el axioma de transitividad?
El axioma de transitividad se usa para establecer relaciones entre diferentes objetos y establecer órdenes y jerarquías. Por ejemplo, si se tiene que A es mayor que B y B es mayor que C, entonces se puede concluir que A es mayor que C.
¿Qué es la teoría de conjuntos?
La teoría de conjuntos es una rama de la matemática que estudia las propiedades y relaciones de los conjuntos.
¿Qué es el razonamiento deductivo?
El razonamiento deductivo es un proceso lógico en el que se parte de premisas para llegar a una conclusión.
Deja una respuesta