Aplicando el teorema: todo lo que necesitas saber

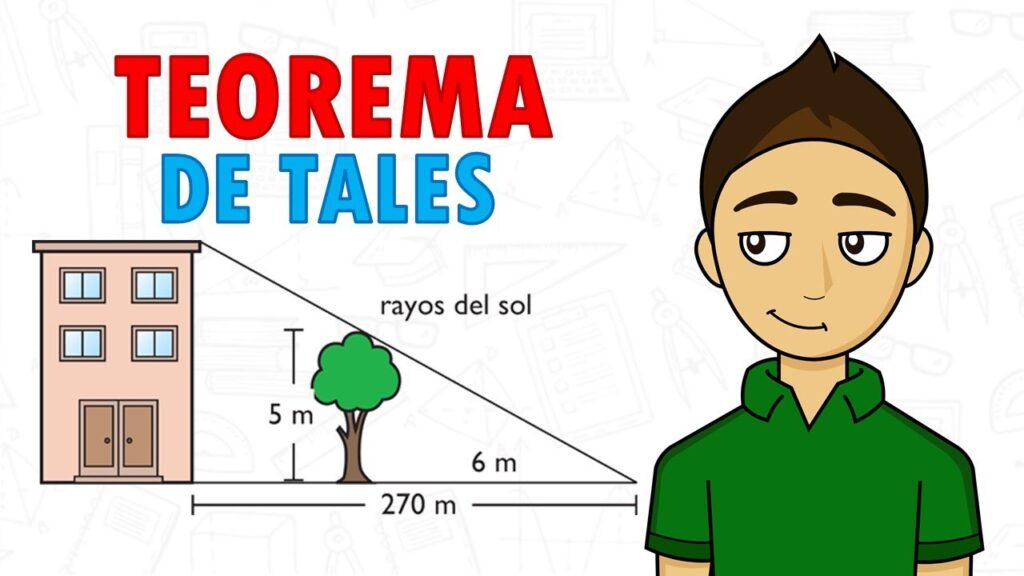
¿Qué es un teorema?

Un teorema es una afirmación matemática que ha sido demostrada como verdadera. Es un enunciado que puede ser usado para deducir otros hechos. A menudo, los teoremas son utilizados para demostrar resultados importantes en matemáticas.

¿Qué es el teorema de Pitágoras?

El teorema de Pitágoras es uno de los teoremas más conocidos en matemáticas. Afirma que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo del triángulo) es igual a la suma de los cuadrados de los otros dos lados.

Este teorema es importante porque nos permite encontrar la longitud de un lado desconocido de un triángulo rectángulo si conocemos las longitudes de los otros dos lados.

¿Cómo se aplica el teorema de Pitágoras?

Para aplicar el teorema de Pitágoras, primero debemos identificar qué lado es la hipotenusa y cuáles son los otros dos lados. Luego, podemos utilizar la fórmula del teorema de Pitágoras para encontrar la longitud del lado desconocido.

Por ejemplo, si tenemos un triángulo rectángulo con una hipotenusa de 5 y un lado de 3, podemos encontrar la longitud del otro lado utilizando la fórmula:

5^2 = 3^2 + x^2

25 = 9 + x^2

16 = x^2

x = 4

Por lo tanto, el otro lado del triángulo rectángulo tiene una longitud de 4.

¿Qué otros teoremas son importantes en matemáticas?

Además del teorema de Pitágoras, hay muchos otros teoremas importantes en matemáticas. Algunos de ellos incluyen:

- El teorema de Euclides: Este teorema establece que existen infinitos números primos.
- El teorema de Fermat: Este teorema establece que no existen soluciones enteras para la ecuación x^n + y^n = z^n cuando n es mayor que 2.
- El teorema de los senos: Este teorema establece que en cualquier triángulo, la proporción entre la longitud de un lado y el seno del ángulo opuesto es constante.
- El teorema de los cosenos: Este teorema establece que en cualquier triángulo, la suma de los cuadrados de los dos lados más cortos es igual al cuadrado del lado más largo menos el doble del producto de los dos lados más cortos y el coseno del ángulo entre ellos.

¿Por qué es importante conocer los teoremas en matemáticas?

Conocer los teoremas en matemáticas es importante porque nos permite entender mejor los conceptos y aplicaciones de las matemáticas. Los teoremas también nos proporcionan herramientas para resolver problemas y demostrar resultados importantes.

Además, los teoremas son fundamentales para el desarrollo de muchas áreas de la ciencia y la tecnología. Por ejemplo, el teorema de Pitágoras es utilizado en la construcción de edificios y puentes, mientras que el teorema de Fermat es utilizado en la criptografía.

Conclusión

Los teoremas son afirmaciones matemáticas importantes que han sido demostradas como verdaderas. Conocer los teoremas nos permite entender mejor los conceptos y aplicaciones de las matemáticas, y nos proporciona herramientas para resolver problemas y demostrar resultados importantes. Desde el teorema de Pitágoras hasta el teorema de Fermat, hay muchos teoremas importantes en matemáticas que tienen aplicaciones en la ciencia y la tecnología.

Preguntas frecuentes

1. ¿Cómo se demuestra un teorema?

Un teorema se demuestra por medio de una demostración matemática rigurosa, que utiliza la lógica y las matemáticas para establecer la verdad del enunciado.

2. ¿Qué es un corolario?

Un corolario es una proposición que sigue directamente de un teorema previamente demostrado.

3. ¿Cuál es el teorema más importante en matemáticas?

Es difícil determinar cuál es el teorema más importante en matemáticas, ya que hay muchos teoremas importantes que han tenido un gran impacto en la ciencia y la tecnología.

4. ¿Cómo se diferencian los teoremas de los axiomas?

Los axiomas son proposiciones que se asumen como verdaderas sin necesidad de demostración, mientras que los teoremas son proposiciones que han sido demostradas como verdaderas.

5. ¿Qué es un teorema condicional?

Un teorema condicional es un teorema que establece que si se cumple una cierta condición, entonces se cumple una cierta consecuencia matemática.