Aplicaciones de Álgebra Booleana: Simplifica tus circuitos

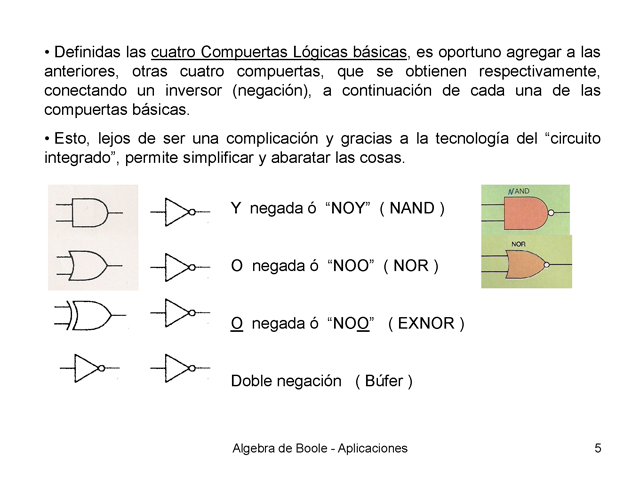
En el mundo de la electrónica, la simplificación de circuitos es una tarea fundamental para el diseño y construcción de cualquier dispositivo. Para ello, se utiliza una rama de las matemáticas conocida como álgebra booleana, que permite reducir complejos sistemas de ecuaciones a formas más simples y manejables.

En este artículo vamos a explorar algunas de las aplicaciones más comunes del álgebra booleana en el diseño de circuitos electrónicos, así como algunos ejemplos prácticos que ilustran su utilidad.

¿Qué es el álgebra booleana?

El álgebra booleana es una rama de las matemáticas que se centra en el estudio de los sistemas lógicos binarios, es decir, en los que sólo existen dos estados posibles: verdadero o falso, 1 o 0, encendido o apagado. A partir de esta base, se pueden establecer una serie de operaciones lógicas, como la negación, la conjunción o la disyunción, que permiten la simplificación de sistemas complejos.

Aplicaciones del álgebra booleana en la electrónica

La aplicación más evidente del álgebra booleana en la electrónica es la simplificación de circuitos. Cuando se trabaja con sistemas de múltiples componentes, es necesario reducirlos a su mínima expresión para evitar errores de diseño o de funcionamiento. Para ello, se utilizan las leyes de De Morgan, que permiten transformar operaciones lógicas complejas en formas más simples.

Otra aplicación del álgebra booleana es el diseño de circuitos combinacionales y secuenciales. Los circuitos combinacionales son aquellos en los que la salida depende únicamente de las entradas, mientras que los secuenciales incorporan algún tipo de memoria o temporización. En ambos casos, el álgebra booleana es fundamental para establecer las ecuaciones que describen su funcionamiento y simplificarlas para su implementación.

Ejemplos prácticos de álgebra booleana en la electrónica

Para ilustrar las aplicaciones del álgebra booleana en la electrónica, vamos a ver algunos ejemplos prácticos de simplificación de circuitos.

Circuito AND

El circuito AND es un circuito combinacional que tiene dos entradas y una salida. La salida sólo será verdadera si ambas entradas son verdaderas. La ecuación que describe su funcionamiento es:

```
Salida = A AND B
```

Utilizando las leyes de De Morgan, podemos simplificar esta ecuación de la siguiente forma:

```
Salida = NOT(NOT(A) OR NOT(B))
```

De esta forma, podemos implementar el circuito AND utilizando dos puertas OR y una puerta NOT, en lugar de dos puertas AND.

Circuito contador

Un circuito contador es un circuito secuencial que se utiliza para contar impulsos de reloj. Está compuesto por una serie de flip-flops que se van activando sucesivamente. La ecuación que describe su funcionamiento es:

```
Q1 = D
Q2 = Q1
Q3 = (Q1 AND Q2) OR D
Q4 = (Q1 AND Q2 AND Q3) OR (NOT(Q1) AND NOT(Q2) AND NOT(Q3))
```

Utilizando las leyes de De Morgan, podemos simplificar esta ecuación de la siguiente forma:

```
Q1 = D
Q2 = Q1
Q3 = Q1 XOR Q2 XOR D
Q4 = (Q1 AND Q2 AND Q3) OR (NOT(Q1) AND NOT(Q2) AND NOT(Q3))
```

De esta forma, hemos simplificado la ecuación del circuito contador y lo hemos hecho más fácil de implementar.

Conclusión

El álgebra booleana es una herramienta fundamental en el diseño y construcción de circuitos electrónicos. Permite simplificar sistemas complejos y establecer ecuaciones que describan su funcionamiento de forma clara y concisa. Además, su uso es esencial para la implementación de circuitos combinacionales y secuenciales.

Preguntas frecuentes

¿Qué es un circuito combinacional?

Un circuito combinacional es aquel en el que la salida sólo depende de las entradas, es decir, no hay ningún tipo de memoria o temporización involucrado.

¿Qué es un circuito secuencial?

Un circuito secuencial es aquel en el que la salida depende de las entradas y del estado actual del circuito, es decir, hay algún tipo de memoria o temporización involucrado.

¿Qué son las leyes de De Morgan?

Las leyes de De Morgan son dos reglas que permiten transformar operaciones lógicas complejas en formas más simples. La primera ley establece que la negación de una conjunción es igual a la disyunción de las negaciones de cada término. La segunda ley establece que la negación de una disyunción es igual a la conjunción de las negaciones de cada término.

¿Qué son los flip-flops?

Los flip-flops son elementos de memoria que se utilizan en los circuitos secuenciales. Permiten almacenar un estado y cambiarlo en función de las entradas y del impulso de reloj.

¿Cómo puedo aprender más sobre álgebra booleana?

Existen numerosos recursos en línea disponibles para aprender más sobre álgebra booleana, desde tutoriales y ejercicios prácticos hasta cursos completos. También es recomendable consultar libros de referencia en el campo de la electrónica digital.