Algebra booleana: la clave para entender la electrónica digital

La electrónica digital es una de las tecnologías más importantes de nuestra era. Desde los teléfonos inteligentes hasta los sistemas informáticos más complejos, todo se basa en los principios de la electrónica digital. Y uno de los conceptos más importantes de esta tecnología es el álgebra booleana. En este artículo, vamos a explorar qué es el álgebra booleana y por qué es tan importante para la electrónica digital.

¿Qué es el álgebra booleana?

El álgebra booleana es una rama de la matemática que se ocupa de las operaciones lógicas y las relaciones booleanas. En términos más simples, es un sistema matemático que se utiliza para manipular y operar con valores booleanos (verdaderos o falsos). El álgebra booleana se utiliza en la electrónica digital para diseñar y construir circuitos digitales y para programar sistemas informáticos.

¿Por qué es importante el álgebra booleana?

El álgebra booleana es fundamental para la electrónica digital porque permite la creación de circuitos y sistemas informáticos que funcionan con una precisión y velocidad increíblemente altas. Los valores booleanos son la base de la electrónica digital y se utilizan para representar el estado de los dispositivos electrónicos. Por ejemplo, un interruptor puede estar encendido o apagado, lo que se representa como verdadero o falso. Los valores booleanos se utilizan para representar cualquier estado en la electrónica digital.

Operaciones booleanas

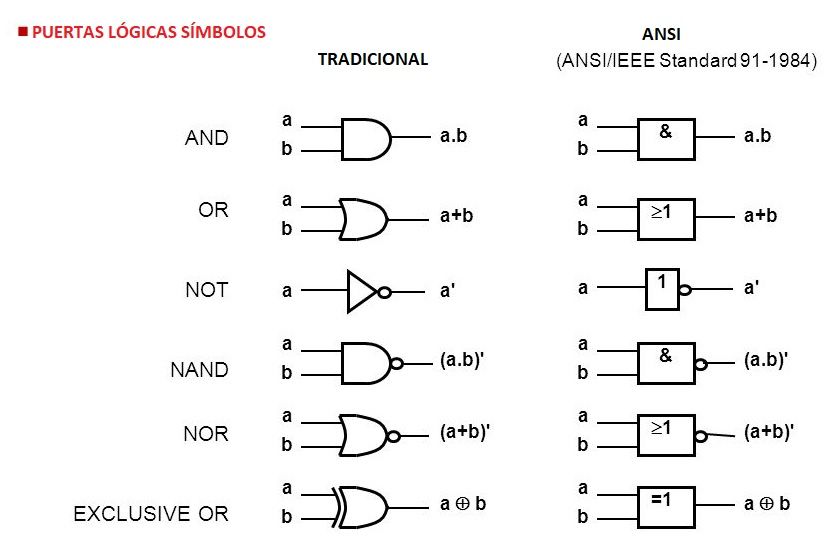
Existen tres operaciones básicas en el álgebra booleana: AND, OR y NOT.

AND

La operación AND se utiliza para determinar si dos valores booleanos son verdaderos. Si ambos valores son verdaderos, el resultado es verdadero. Si uno o ambos valores son falsos, el resultado es falso.

Ejemplo:

Si tenemos dos valores booleanos, A y B, y A es verdadero (1) y B es falso (0), el resultado de la operación AND sería falso (0).

A AND B = 0

OR

La operación OR se utiliza para determinar si al menos uno de los valores booleanos es verdadero. Si uno o ambos valores son verdaderos, el resultado es verdadero. Si ambos valores son falsos, el resultado es falso.

Ejemplo:

Si tenemos dos valores booleanos, A y B, y A es verdadero (1) y B es falso (0), el resultado de la operación OR sería verdadero (1).

A OR B = 1

NOT

La operación NOT se utiliza para invertir el valor booleano de un dispositivo o circuito. Si el valor booleano es verdadero, la operación NOT lo convierte en falso. Si el valor booleano es falso, la operación NOT lo convierte en verdadero.

Ejemplo:

Si tenemos un valor booleano A y A es verdadero (1), el resultado de la operación NOT sería falso (0).

NOT A = 0

Aplicaciones del álgebra booleana

El álgebra booleana se utiliza en muchas aplicaciones diferentes. Algunas de las aplicaciones más comunes incluyen:

Circuitos lógicos

El álgebra booleana se utiliza para diseñar y construir circuitos lógicos que se utilizan en la electrónica digital. Un circuito lógico es un circuito que realiza una operación lógica en uno o más valores booleanos.

Programación

El álgebra booleana se utiliza en la programación de sistemas informáticos. Los valores booleanos se utilizan para representar el estado de los dispositivos y los circuitos, y las operaciones booleanas se utilizan para manipular estos valores.

Redes de computadoras

El álgebra booleana se utiliza en la creación y configuración de redes de computadoras. Los valores booleanos se utilizan para representar los estados de los dispositivos de red, y las operaciones booleanas se utilizan para determinar cómo se comunican estos dispositivos.

Conclusión

El álgebra booleana es una parte fundamental de la electrónica digital. Se utiliza para diseñar y construir circuitos digitales, programar sistemas informáticos y configurar redes de computadoras. Si quieres entender cómo funciona la electrónica digital, es esencial que comprendas los conceptos básicos del álgebra booleana.

Preguntas frecuentes

1. ¿Qué es un valor booleano?

Un valor booleano es un valor que puede ser verdadero o falso. En la electrónica digital, los valores booleanos se utilizan para representar el estado de los dispositivos electrónicos.

2. ¿Qué son las operaciones booleanas?

Las operaciones booleanas son las operaciones lógicas que se utilizan para manipular los valores booleanos. Las operaciones básicas son AND, OR y NOT.

3. ¿Para qué se utiliza el álgebra booleana?

El álgebra booleana se utiliza en la electrónica digital para diseñar y construir circuitos digitales, programar sistemas informáticos y configurar redes de computadoras.

4. ¿Cuáles son las aplicaciones del álgebra booleana?

Las aplicaciones del álgebra booleana incluyen circuitos lógicos, programación y redes de computadoras.

5. ¿Cómo se utilizan las operaciones booleanas?

Las operaciones booleanas se utilizan para manipular y operar con valores booleanos. Las operaciones básicas son AND, OR y NOT.