Descubre la lógica proposicional: teoría y ejemplos
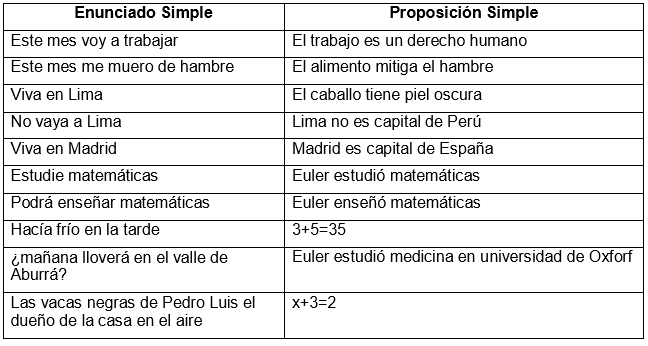
La lógica proposicional es una rama de la filosofía y las matemáticas que se centra en el estudio de las proposiciones y sus relaciones lógicas. En términos simples, la lógica proposicional se ocupa de la forma en que las proposiciones se combinan para formar argumentos válidos. En este artículo, exploraremos la teoría detrás de la lógica proposicional y proporcionaremos algunos ejemplos para ayudar a ilustrar sus conceptos clave.
¿Qué es la lógica proposicional?
La lógica proposicional es una rama de la lógica formal que se centra en las proposiciones, que son declaraciones que pueden ser verdaderas o falsas. Estas proposiciones se combinan para formar argumentos, que son secuencias de proposiciones que pretenden demostrar una afirmación. La lógica proposicional estudia cómo estas proposiciones se relacionan entre sí y cómo se pueden usar para construir argumentos válidos.
La lógica proposicional se ocupa principalmente de los conectivos lógicos, que son palabras o símbolos que se utilizan para conectar proposiciones. Los conectivos lógicos más comunes son "y" (conjugación), "o" (disyunción), "si... entonces" (implicación) y "no" (negación). Estos conectivos se utilizan para construir fórmulas lógicas, que son combinaciones de proposiciones y conectivos.
Fórmulas lógicas
Las fórmulas lógicas son la base de la lógica proposicional. Son combinaciones de proposiciones y conectivos lógicos que se utilizan para construir argumentos válidos. Las fórmulas lógicas se construyen utilizando una sintaxis específica que sigue ciertas reglas.
Por ejemplo, la fórmula lógica "p y q" representa la conjunción de las proposiciones "p" y "q". La fórmula lógica "p o q" representa la disyunción de las proposiciones "p" y "q". La fórmula lógica "si p, entonces q" representa la implicación de la proposición "p" en la proposición "q". La fórmula lógica "no p" representa la negación de la proposición "p".
Tablas de verdad
Las tablas de verdad son herramientas útiles para analizar fórmulas lógicas. Una tabla de verdad es una tabla que muestra todas las posibles combinaciones de verdad y falsedad de las proposiciones que aparecen en una fórmula lógica. Cada fila de la tabla representa una combinación diferente de verdad y falsedad de las proposiciones, y cada columna representa una proposición diferente en la fórmula.
Por ejemplo, la tabla de verdad para la fórmula lógica "p y q" se muestra a continuación:
| p | q | p y q |
|---|---|-------|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
La tabla de verdad muestra que la fórmula "p y q" es verdadera solo cuando ambas proposiciones "p" y "q" son verdaderas.
Ejemplos de lógica proposicional
Veamos algunos ejemplos de cómo se puede aplicar la lógica proposicional en la vida cotidiana.
Ejemplo 1: Comprar un coche
Imagina que estás buscando un coche nuevo. Tienes tres opciones: un coche rojo, un coche azul y un coche verde. También tienes dos criterios que son importantes para ti: el precio y la eficiencia de combustible. Puedes representar tus opciones y criterios en forma de proposiciones:
- P: El coche es rojo.
- Q: El coche es azul.
- R: El coche es verde.
- S: El coche es barato.
- T: El coche es eficiente en combustible.
Puedes construir una fórmula lógica para representar tu decisión de compra:
"(P y S) o (Q y T) o (R y T)"
Esta fórmula lógica representa la disyunción de tres conjunciones. La primera conjunción representa la opción del coche rojo y barato, la segunda representa la opción del coche azul y eficiente en combustible, y la tercera representa la opción del coche verde y eficiente en combustible. Con esta fórmula lógica, puedes evaluar cada opción y determinar cuál cumple con tus criterios.
Ejemplo 2: Programación de computadoras
La lógica proposicional también es útil en la programación de computadoras. Los programas informáticos se basan en la lógica proposicional para tomar decisiones y realizar tareas. Por ejemplo, un programa de chat podría usar la siguiente fórmula lógica para decidir si mostrar un mensaje:
"(amigo_en_línea y no_estoy_ocupado) o (mensaje_no_leído)"
Esta fórmula lógica representa la disyunción de dos conjunciones. La primera conjunción representa la condición de que tu amigo esté en línea y que no estés ocupado. La segunda conjunción representa la condición de que haya un mensaje no leído. Si se cumple una de estas condiciones, el programa mostrará un mensaje.
Conclusión
La lógica proposicional es una herramienta útil para analizar proposiciones y construir argumentos válidos. Se basa en el uso de conectivos lógicos y fórmulas lógicas para representar relaciones lógicas entre proposiciones. Las tablas de verdad son una herramienta útil para analizar fórmulas lógicas y determinar su validez. La lógica proposicional también se aplica en la vida cotidiana y en la programación de computadoras.
Preguntas frecuentes
1. ¿Qué es la lógica formal?
La lógica formal es una rama de la filosofía y las matemáticas que se centra en el estudio de la validez de los argumentos. Se basa en el uso de reglas formales para analizar proposiciones y construir argumentos válidos.
2. ¿Qué son los conectivos lógicos?
Los conectivos lógicos son palabras o símbolos que se utilizan para conectar proposiciones en la lógica proposicional. Los conectivos lógicos más comunes son "y" (conjugación), "o" (disyunción), "si... entonces" (implicación) y "no" (negación).
3. ¿Qué es una tabla de verdad?
Una tabla de verdad es una tabla que muestra todas las posibles combinaciones de verdad y falsedad de las proposiciones que aparecen en una fórmula lógica. Cada fila de la tabla representa una combinación diferente de verdad y falsedad de las proposiciones, y cada columna representa una proposición diferente en la fórmula.
4. ¿Cómo se aplica la lógica proposicional en la vida cotidiana?
La lógica proposicional se aplica en la vida cotidiana en la toma de decisiones y la resolución de
Deja una respuesta